訊號處理/數字濾波器

數字濾波器

數字濾波器本質上是取樣系統。輸入和輸出訊號由時間距離相等的樣本表示。

有限脈衝響應 (FIR) 濾波器

有限脈衝響應 (FIR) 濾波器的特點是，時間響應僅取決於輸入訊號的給定數量的最後一個樣本。換句話說：一旦輸入訊號降至零，濾波器輸出將在給定數量的取樣週期後也降至零。

輸出 $y(k)$ 由最後一個輸入樣本的線性組合給出 $x(k-i)$ .

y(k)=\sum _{i=0}^{N-1}b(i)\cdot x(k-i)

係數 $b(i)$ 給出了組合的權重。它們還對應於 z 域濾波器傳遞函式的分子係數。

下圖顯示了一個階數為 $N$ 的 FIR 濾波器

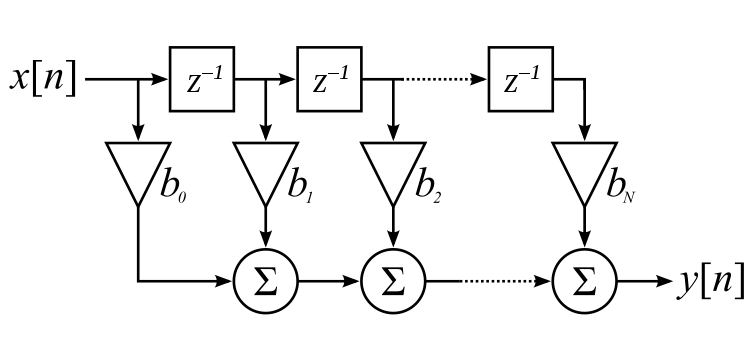
對於線性相位濾波器，係數值圍繞中間係數對稱，並且可以將延遲線摺疊回該中間點以減少乘法次數。

FIR 濾波器的傳遞函式只包含分子。這對應於全零濾波器。

FIR 濾波器通常需要高階，通常達到數百。因此，選擇這種濾波器將需要大量的硬體或 CPU。儘管如此，選擇 FIR 濾波器實現的一個原因是能夠實現線性相位響應，這在某些情況下可能是一個要求。然而，濾波器設計者可以選擇 IIR 濾波器，在通帶中具有良好的相位線性，例如貝塞爾濾波器，或者設計一個全通濾波器來校正標準 IIR 濾波器的相位響應。

平均濾波器

顧名思義，平均濾波器（或簡單移動平均濾波器，SMA 濾波器）計算訊號的最後一個 $N$ 個樣本的平均值

y(k)={\frac {1}{N}}\cdot \sum _{i=0}^{N-1}x(k-i)

它是 FIR 濾波器的最簡單形式，所有係數都相等。

平均濾波器的傳遞函式由下式給出

{\begin{aligned}H(z)&={\frac {1}{N}}\cdot \sum _{i=0}^{N-1}z^{-i}\\&={\frac {1}{N}}\cdot \left({\frac {1-z^{-N}}{1-z^{-1}}}\right)\end{aligned}}

平均濾波器的傳遞函式在頻域上有 $N$ 個等間距的零點。但是，直流處的零點被濾波器的極點掩蓋了。因此，在直流處有一個更大的瓣，它代表了濾波器的通帶。

加權移動平均

加權移動平均濾波器給樣本新增權重，以便對其中一些樣本給予更多重視。

y(k)={\frac {\sum _{i=0}^{N-1}w(k-i)\cdot x(k-i)}{\sum _{i=0}^{N-1}w(k-i)}}

權重可以線性變化或指數變化。

遞迴實現

移動平均濾波器的遞迴實現基於這樣一個事實，即兩個連續輸出樣本的輸出由相同的一組輸入樣本的總和構成，只是第一個和最後一個樣本除外。

y(k)=y(k-1)+{\frac {1}{N}}\cdot [x(k)-x(k-(N-1))]

級聯積分梳狀 (CIC) 實現

級聯積分梳狀濾波器 (CIC) 是一種特殊的技術，用於實現串聯放置的平均濾波器。平均濾波器的串聯放置增強了直流處的第一個瓣，相對於所有其他瓣。

CIC 濾波器實現了 $N$ 個平均濾波器的傳遞函式，每個濾波器計算 $RM$ 個樣本的平均值。因此，它的傳遞函式由下式給出：

H(z)=\left({\frac {1-z^{-R\cdot M}}{1-z^{-1}}}\right)^{N}

CIC 濾波器用於將訊號樣本數量減少 R 倍，或者換句話說，以較低的頻率對訊號進行重新取樣，丟棄 R-1 個樣本中的 R 個樣本。因子 M 指示訊號使用了第一個瓣的多少部分。平均濾波級數 N 指示其他頻段被抑制的程度，以犧牲在直流附近的傳輸函式不太平坦為代價。

CIC 結構允許僅使用加法器和暫存器來實現整個系統，而不使用任何在硬體方面貪婪的乘法器。

R 倍的下采樣允許將訊號解析度提高 log₂(R) 位。

IIR 濾波器

典型濾波器

典型濾波器使用與濾波器階數相等的延遲元件數量來實現濾波器傳輸函式，每個分子係數一個乘法器，每個分母系數一個乘法器，以及一系列加法器。類似於有源濾波器的典型結構，這種型別的電路已被證明對元件值非常敏感：係數的微小變化會對傳輸函式產生很大影響。

這裡也是如此，有源濾波器設計已從典型濾波器轉移到其他結構，例如“二階節鏈”或“蛙跳濾波器”。

二階節鏈

“二階節”，通常稱為“雙二階”，實現二階傳輸函式。濾波器的傳輸函式可以分解為傳輸函式的乘積，每個傳輸函式都與一對極點和可能的一對零點相關聯。如果傳輸函式的階數為奇數，則必須在鏈中新增一個一階節。該節與實極點和可能存在的實零點相關聯。

最著名的濾波器雙二階結構是

直接形式 1
直接形式 2
直接形式 1 轉置
直接形式 2 轉置

下圖所示的直接形式 2 轉置在所需硬體以及訊號和係數量化方面特別有趣。

數字蛙跳濾波器

濾波器結構

數字蛙跳濾波器基於對模擬有源蛙跳濾波器的模擬。這種選擇的動機是為了繼承原始梯形電路的優異通帶靈敏度特性。

以下 4 階全極點低通蛙跳濾波器

可以透過將模擬積分器替換為累加器來實現為數位電路。

將模擬積分器替換為累加器對應於將 Z 變換簡化為 z = 1 + sT，它們是泰勒級數中 z = exp(sT) 的前兩個項。對於取樣頻率遠高於訊號頻寬的濾波器，這種近似足夠好。

傳輸函式

上述濾波器的狀態空間表示可以寫成

{\begin{array}{ccrcccccc}z\cdot {\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&=&{\begin{bmatrix}1-{\frac {T}{t_{1}}}&-{\frac {T}{t_{1}}}&0&0\\{\frac {T}{t_{2}}}&1&-{\frac {T}{t_{2}}}&0\\0&{\frac {T}{t_{3}}}&1&-{\frac {T}{t_{3}}}\\0&0&{\frac {T}{t_{4}}}&1-{\frac {T}{t_{4}}}\end{bmatrix}}&\cdot &{\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&+&{\begin{bmatrix}{\frac {T}{t_{1}}}\\0\\0\\0\end{bmatrix}}&\cdot &U_{in}\\U_{out}&=&{\begin{bmatrix}0&0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &U_{in}\end{array}}

從這個方程組可以寫出 A、B、C、D 矩陣：

A={\begin{bmatrix}1-{\frac {T}{t_{1}}}&-{\frac {T}{t_{1}}}&0&0\\{\frac {T}{t_{2}}}&1&-{\frac {T}{t_{2}}}&0\\0&{\frac {T}{t_{3}}}&1&-{\frac {T}{t_{3}}}\\0&0&{\frac {T}{t_{4}}}&1-{\frac {T}{t_{4}}}\end{bmatrix}}

B={\begin{bmatrix}{\frac {T}{t_{1}}}\\0\\0\\0\end{bmatrix}}

C={\begin{bmatrix}0&0&0&1\end{bmatrix}}

D={\begin{bmatrix}0\end{bmatrix}}

有了這個表示，就可以使用像 Octave 或 Matlab 這樣的訊號處理工具來繪製濾波器的頻率響應或檢查其零點和極點。

在數字跳躍濾波器中，係數的相對值決定了傳遞函式的形狀（巴特沃斯，切比雪夫，…），而它們的幅度則決定了截止頻率。將所有係數除以 2 會使截止頻率降低一個倍頻程（也是 2 倍）。

一個特例是巴特沃斯 3 階濾波器，其時間常數的相對值為 1、1/2 和 1。因此，這個濾波器可以在硬體中實現，無需任何乘法器，而使用移位代替。

自迴歸濾波器 (AR)

自迴歸 (AR) 模型是以下形式的處理模型

u(n)=\sum _{m=1}^{M}a^{*}(m)u(n-m)+x(n)

其中u(n)是模型的輸出，x(n)是模型的輸入，u(n - m)是模型輸出值的先前樣本。這些濾波器被稱為“自迴歸”，因為輸出值是基於先前輸出值的迴歸來計算的。AR 過程可以用全極點濾波器來表示。

ARMA 濾波器

自迴歸移動平均 (ARMA) 濾波器是 AR 和 MA 濾波器的組合。濾波器的輸出作為加權輸入樣本和加權輸出樣本的線性組合給出

y(n)=\sum _{m=0}^{M}a^{*}(m)x(n-m)+\sum _{k=1}^{K}b^{*}(k)y(n-k)

ARMA 過程可以被認為是數字 IIR 濾波器，具有極點和零點。

Yule-Walker 方程

AR 濾波器在許多情況下是首選，因為它們可以使用Yule-Walker 方程進行分析。另一方面，MA 和 ARMA 過程可以透過複雜的非線性方程進行分析，這些方程難以研究和建模。

如果我們有一個具有抽頭權重係數a（a(n), a(n - 1), ... 的向量）的 AR 過程，輸入為x(n)，輸出為y(n)，我們可以使用 Yule-Walker 方程。我們說 σ_x² 是輸入訊號的方差。我們把輸入資料訊號視為隨機訊號，即使它是確定性訊號，因為我們不知道它的值，直到我們收到它。我們可以將 Yule-Walker 方程表示為

[Yule-Walker 方程]