A-level 數學/OCR/C2/三角函式

角的三角函式比

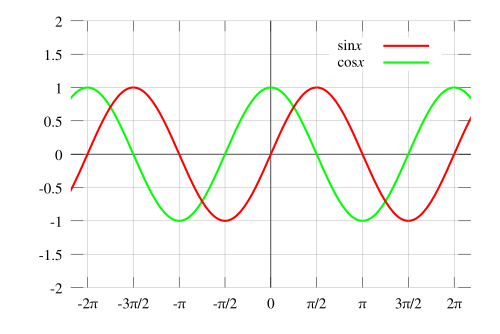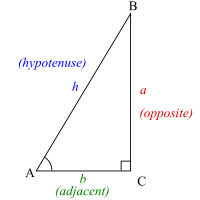
我們使用左側的三角形來定義三個基本的三角函式比，使用角 A。一個好的記憶方法是縮略詞 SOHCAHTOA，正弦對邊比斜邊，餘弦鄰邊比斜邊，正切對邊比鄰邊。請記住，如果使用計算器獲取三角函式比的值，請確保它處於正確的模式；如果角度是弧度，它應該處於弧度模式；如果角度是度數，它應該處於度數模式。您可以使用每個函式的倒數找到與值相對應的角度，通常列為 $\cos ^{-1},\sin ^{-1},\tan ^{-1}$ 在你的計算器上，關於反三角函式的正式討論將在核心 3 中進行。正切圖中的藍色虛線是正切函式的漸近線。正切函式在這些點上將沒有定義，因為在這些點上餘弦圖是零，請參閱正切恆等式。

函式	書寫	定義	圖
餘弦	$\cos \theta \,$	${\frac {Adjacent}{Hypotenuse}}$
正弦	$\sin \theta \,$	${\frac {Opposite}{Hypotenuse}}$
正切	$\tan \theta \,$	${\frac {Opposite}{Adjacent}}$

CAST模型

CAST 模型用於顯示三角函式比在哪個象限為正。一個記憶方法是 All Students Take Core 4。4 表示餘弦在第四象限。另外，您需要知道 sin(x) = sin(π rad 或 180° - x) = c，cos(x) = cos(2π rad 或 360° - x) = c，tan(x) = tan(π rad 或 180° + x)= c。這很重要，因為如果 sin(x) = 1/2，並且它在 0° 和 360° 之間，那麼 x 可以是 30° 或 150°。

重要的三角函式值

以下是具有常見三角函式值的表格（圓圈標有相同的值），您需要記住這些值。 $\theta \,$ $rad\,$ $\sin \theta \,$ $\cos \theta \,$ $\tan \theta \,$ $0^{\circ }$ 0 0 1 0 $30^{\circ }$ ${\frac {\pi }{6}}$ ${\frac {1}{2}}$ ${\frac {\sqrt {3}}{2}}$ ${\frac {1}{\sqrt {3}}}$ $45^{\circ }$ ${\frac {\pi }{4}}$ ${\frac {\sqrt {2}}{2}}$ ${\frac {\sqrt {2}}{2}}$ $1\,$ $60^{\circ }$ ${\frac {\pi }{3}}$ ${\frac {\sqrt {3}}{2}}$ ${\frac {1}{2}}$ ${\sqrt {3}}$ $90^{\circ }$ ${\frac {\pi }{2}}$ 1 0 無

餘弦定理

勾股定理只適用於直角三角形，而餘弦定理適用於任何三角形。 當你有一個直角三角形時，它會簡化為與勾股定理相同的公式。 對於任何三角形 ABC，其角度測量值為 $\alpha$, $\beta$, $\gamma$ 和邊長 a、b、c。

$a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,$
$b^{2}=a^{2}+c^{2}-2ac\cos \beta \,$
$c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,$

示例

當 a = 4 cm，b = 8 cm 且 $\gamma$ 等於 $64^{\circ }$ 時，c 的值為多少？ $c^{2}=4^{2}+8^{2}-2\times 4\times 8\cos 64^{\circ }\,$

$c^{2}=53\,$

$c\approx 7.28\ cm$

正弦定理

對於任意三角形 ABC，其角測量值為 $\alpha$，$\beta$，$\gamma$ 和邊長為 a、b、c。

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

示例 如果角 α 為 $45^{\circ }$，角 β 為 $24^{\circ }$，邊 b 為 3 cm，那麼邊 a 的長度是多少？

${\frac {a}{\sin 45^{\circ }}}={\frac {3}{\sin 24^{\circ }}}$

$a\times \sin 24^{\circ }=3\times \sin 45^{\circ }$

$a={\frac {3\times \sin 45^{\circ }}{\sin 24^{\circ }}}\approx 5.22\ {\mbox{cm}}$

三角形面積

對於任何三角形，面積等於兩邊乘積的一半乘以夾角的正弦值。如果夾角是直角，則公式簡化為直角三角形面積公式，因為 $\sin 90^{\circ }=1$

$Area={\frac {1}{2}}bc\sin \alpha \,$

$Area={\frac {1}{2}}ac\sin \beta \,$

$Area={\frac {1}{2}}ab\sin \gamma \,$

示例

當a = 4 cm，b = 8 cm，並且 $\gamma$ 等於 $20^{\circ }$ 時，三角形的面積是多少？

$Area={\frac {1}{2}}\times 4\times 8\times \sin 20^{\circ }\,\approx 5.47\ {\mbox{cm}}^{2}$

勾股定理

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

證明

我們使用勾股定理

$a^{2}+b^{2}=c^{2}\,$

現在我們除以 $c^{2}$

${\frac {a^{2}}{c^{2}}}+{\frac {b^{2}}{c^{2}}}={\frac {c^{2}}{c^{2}}}\,$

我們得到

${\frac {a^{2}}{c^{2}}}+{\frac {b^{2}}{c^{2}}}=1\,$

我們可以寫成

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

一種理解這個概念的方法是 $opposite^{2}+adjacent^{2}=hypotenuse^{2}={\frac {opposite^{2}}{hypotenuse^{2}}}+{\frac {adjacent^{2}}{hypotenuse^{2}}}=1$

實際例子

找出所有滿足關係式 $15\sin ^{2}\left(x\right)=\cos \left(x\right)+13$ 的x的值， 其中 0 rad < x < 2π rad.

利用畢達哥拉斯恆等式，我們得到

$15\left(1-\cos ^{2}\left(x\right)\right)=\cos \left(x\right)+13$

現在我們可以簡化

$15\cos ^{2}\left(x\right)-\cos \left(x\right)-2=0$

用 u 代替 cos(x) 更方便

$15u^{2}-u-2=0\,$

然後我們分解表示式

$\left(5u+2\right)\left(3u-1\right)=0$

$\cos \left(x\right)={\frac {-2}{5}}\ or\ {\frac {1}{3}}$

為了確定 x 的值，我們需要使用計算器上的 $\cos ^{-1}\left(x\right)$.

$\cos ^{-1}\left({\frac {-2}{5}}\right)\approx 1.9823\ rad$

$\cos ^{-1}\left({\frac {1}{3}}\right)\approx 1.2310\ rad$

但我們需要記住，在 2π 區間內，餘弦函式在 2π - x 中的值相同。

2π rad - 1.2310 rad = 5.0222 rad

2π rad - 1.9823 rad = 4.3009 rad

因此，完整的答案是 1.2310 rad，1.9823 rad，4.3009 rad 和 5.0222 rad.

正切恆等式

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

證明

$\tan \theta ={\frac {a}{b}}$

然後我們用 c 除分子和分母

$\tan \theta ={\frac {\frac {a}{c}}{\frac {b}{c}}}$

我們可以寫成

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

示例

sin(x) = 4cos(x)，求解 sin(x) 。所有單位都是弧度。

我們兩邊同除以 cos x，得到恆等式

tan(x)=4

我們使用 $tan^{-1}(x)$ 來得到 x = 1.3258 弧度。

現在我們可以解出 sin(x)

sin(x) = 4cos(1.3258 弧度) = 4*.2425 弧度 = .9701 弧度。

這是 C2 (核心數學 2) 模組的一部分，來自 A-level 數學 教材。

多項式除法與因式分解 / 數列與級數 / 對數與指數 / 圓與角 / 積分

附錄 A: 公式