資料科學：入門/像數學家一樣思考

資料科學：入門

第 10 章：像數學家一樣思考

---

貢獻者說明 (章節完成時刪除本節)

首先，請在 Wikibooks 上註冊您的賬戶（並在下方列出您的資訊），以便我們瞭解我們的共同貢獻者。此外，請遵守 Wikibooks 的 編輯指南、風格手冊 和 政策與指南。感謝您的配合。

其次，我們只需要每個章節中簡單、清晰、直接的資訊。我們不是試圖面面俱到或全面覆蓋——本書的價值在於跨學科的簡單綜合。在其他地方可以詳盡地闡述特定主題的深度和複雜性。在您做出貢獻時，請以“初學者的心態”來思考。請也確保每個章節的範圍，以便在一小時的課堂時間內講授。如果一個章節需要超過一小時來教授，它可能過於詳細。

• 在儘可能的情況下，請使用維基百科和維基詞典中定義的術語和概念。這樣，學生就可以參考相應的維基百科/維基詞典頁面，以便更深入地理解概念。

第三，這是一本跨學科的書籍。我們希望幫助人們將資料科學應用於所有領域。因此，我們需要各種各樣的簡單示例和簡單練習。

第四，請遵守每個章節的簡單結構：要點摘要、討論、更多閱讀、練習和參考資料。我們希望“更多閱讀”部分連結到線上資源。參考資料部分可能包含離線資源。要開始一個新頁面，您應該使用來自 這個原型頁面 的維基標記。

第五，與任何維基書籍一樣，請隨時進行更正、擴充套件解釋和必要時的新增，即使它不是“你的”章節。使用討論頁面來解釋可能存在爭議的更改。

第六，一些語法規則

• 請將學生應該學習的關鍵術語和短語用 粗體 表示。
• 使用 'code' 標籤將函式和程式碼片段的名稱放在程式碼中：<code>lm()</code>
• 使用內聯連結 [[ ]] 連結到維基百科、維基詞典、維基共享資源、維基書籍和其他維基媒體基金會屬性。
• 使用引用 (<ref> </ref>) 來引用“外部”來源——無論是線上還是離線。
  • 使用引用模板建立引用：模板：引用書籍、模板：引用網頁、模板：引用期刊
• 如果您想新增影像或圖表，您應該將它上傳到 維基共享資源，而不是上傳到維基書籍。
  • 如果適用，在上傳圖表時新增標籤 {{Created with R}})。
• 如果使用與 R 標準包不同的包，在每個函式後用括號將包名用粗體表示：<code>MCMCprobit()</code> ('''MCMCpack''')
• 您可以使用第三章 資料定義 作為如何撰寫章節的示例。

最後，非常感謝您自願加入我們的團隊！

章節摘要

當資料科學家以數學家的思維方式思考時，他們會從測量和模型的角度進行思考。任務是將問題分解為其基本組成部分；用數值表示這些組成部分；並將這些組成部分組合成對問題及其解決方案的準確表達。

討論

根據 維基百科，數學是關於數量、結構、空間和變化的研究。當這些用於解決實際問題時，被稱為 應用數學。除了這些主要關注點之外，還有一些主題致力於探索從數學核心到其他領域的聯絡：邏輯、集合論，以及最近的不確定性研究。為了本書的目的，我們不會探索數學的最後三個方面。

數量

數量的研究從 數字 開始，首先是熟悉的 自然數 和 整數（“整數”）以及它們的基本算術運算，這些運算在 算術 中得到體現。隨著數字系統的進一步發展，整數被認為是 有理數（“分數”）的子集。反過來，這些有理數包含在 實數 中，實數用於表示 連續 的量。實數被推廣到 複數。

$1,2,3\,...\!$	$...-2,-1,0,1,2\,...\!$	$-2,{\frac {2}{3}},1.21\,\!$	$-e,{\sqrt {2}},3,\pi \,\!$	$2,i,-2+3i,2e^{i{\frac {4\pi }{3}}}\,\!$
自然數	整數	有理數	實數	複數

當以數學家的思維方式思考時，資料科學家需要問自己這樣的問題：“我感興趣的事物將如何用數字表示？”以及“什麼樣的數字最能代表我感興趣的事物？”

結構

許多數學物件的集合都表現出內部的 結構。數學透過對物件應用規則（公理和運算）來揭示這些結構。 代數 是理解數學結構的強大工具。它將 變數 的概念與算術相結合來 解方程。代數被應用於許多不同的、表面上看似無關的問題。其中一些問題包括 環、群、圖 和 域。

${\begin{matrix}(1,2,3)&(1,3,2)\\(2,1,3)&(2,3,1)\\(3,1,2)&(3,2,1)\end{matrix}}$
集合	環	群	圖	域

當以數學家的思維方式思考時，資料科學家需要問自己：“我感興趣的事物內部結構是什麼樣的？” 以及“哪組方程可以揭示這種結構？”

空間

空間 的研究起源於 幾何學，尤其是 歐幾里得幾何學。 三角學 是數學的一個分支，它處理三角形邊和角之間的關係；它將空間和數字結合在一起，包含著名的 勾股定理。空間的高階研究包括高維幾何、 非歐幾里得幾何學、 微分幾何學、 拓撲學、 分形幾何學 以及 Wikipedia:測度論。出於本書的目的，我們不會涵蓋這些更高階的幾何學。

幾何學	三角學	微分幾何學	拓撲學	分形幾何學	測度論

當以數學家的思維方式思考時，資料科學家需要問自己：“我感興趣的事物是否有空間成分（無論是實際的還是理論上的）？” 以及“我如何捕捉和表示這種空間成分？”

變化

理解和描述變化 是科學中的一個常見主題，而 微積分 作為研究它的有力工具而發展起來。 函式 是描述變化量的一個核心概念。許多問題自然地導致一個量與其變化率之間的關係。也就是說，對於非直線，斜率在線上每個點都不同。理解這些變化的斜率在 微分微積分 中被研究。求曲線下方的面積稱為 積分微積分。微積分超出了本書的範圍。

(x, f(x)) 處的切線。曲線在一點處的導數 f′(x) 是該點處與該曲線相切的直線的斜率（上升量除以執行量）。

積分可以被認為是測量由 f(x) 定義的曲線在兩點（這裡為 a 和 b）之間下的面積 S。

以數學家的思維方式思考，資料科學家必須問自己：“我感興趣的事物之間的關係是否隨時間或距離變化？” 以及“我將如何描述這種變化的關係？”

應用數學

應用數學 關注的是 數學方法，這些方法通常用於科學、工程、商業和工業。因此，“應用數學”就是具有專業知識的數學。一般來說，這是資料科學家從事的數學型別。

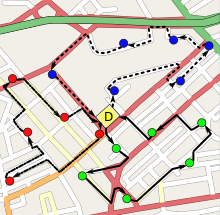
針對 車輛路線問題 的有效解決方案需要數學工具。

對金融市場的建模是透過數學完成的。

作業/練習

本專案#2涵蓋四章。組成3-4人的小組。三人小組的成員可能與專案#1中的小組成員不同。四人小組最多可以有兩名學生重複使用專案#1中的小組成員。這個小組將一起完成整個專案。

1. 複製伽利略的“斜面”實驗。首先設計研究並寫下你的計劃。列出需要的材料，指定要使用的方法，確定要測量的變數，建立資料記錄表，等等。
2. 根據設計進行實驗。拍照。記錄你的資料結果。
3. 將資料輸入R。使用R生成資料的表格並繪製資料圖。看看你是否可以在資料圖上繪製伽利略試圖發現的理論曲線。
4. 準備一個幻燈片演示，其中包括你所用方法的描述、裝置照片、原始資料的表格、分析結果的表格、結果圖、該小組在專案過程中自己學到的關於資料科學的幾件事的清單。

注意：你的小組可以專注於特定任務，但每個人都需要參與作業的所有階段。另外，到目前為止涵蓋的章節並沒有教你完成此作業所需的一切知識。請盡你所能利用你的知識。此作業不僅僅是為了向講師展示你對前幾章內容的學習程度，它本身就是一個學習體驗。此作業的目的是讓學生髮現章節中沒有包含的知識。

版權宣告

您可以

• 分享——複製、分發、展示和執行作品（來自此維基的頁面）
• 混合——改編或製作衍生作品

在以下條件下

• 署名——您必須將此作品歸功於華夏公益教科書。您不能暗示華夏公益教科書以任何方式認可您或您對該作品的使用。
• 相同方式共享——如果您更改、轉換或構建此作品，您只能在與本許可證相同或相似的許可證下分發生成的作品。
• 放棄——如果您獲得版權所有者的許可，上述任何條件都可以被放棄。
• 公有領域——如果作品或其任何部分根據適用法律處於公有領域，則其狀態不受本許可證的影響。
• 其他權利——本許可證不以任何方式影響以下任何權利

• 您的合理使用權或其他適用的版權例外和限制；
• 作者的署名權；
• 他人可能對作品本身或作品的使用方式擁有的權利，例如公開權或隱私權。

• 通知——對於任何再利用或分發，您必須向他人明確說明此作品的許可條款。執行此操作的最佳方法是連結到以下網頁。

http://creativecommons.org/licenses/by-nc-sa/3.0/