分形/複平面上的迭代/花瓣
Leau-Fatou 花的花瓣

"花瓣...有趣之處不僅在於它們對拋物點附近出現的動力學提供了相當直觀的理解,而且在於 f0 在花瓣上的動力學可以線性化,即它與由 T(w) := w + 1 定義的 C 的位移對映 T 共軛。"(Laurea Triennale[1])
- 花瓣沒有統一的定義
- "花瓣是 不變的約旦域"(R PEREZ-MARCO[2] (其中 q 是子週期。並且拋物線 c 引數是曼德布羅特集的父元件和子元件之間的根點)
- 花瓣是陷阱,它捕獲任何趨向於拋物點的軌道
- 花瓣是花的一部分
花的花瓣可以是
- 吸引/排斥
- 小/α/大/(小的吸引花瓣與排斥花瓣不重疊,但大的則重疊)
每個花瓣在 f^週期下是不變的。換句話說,它被 f^週期對映到自身。
吸引花瓣 P 是
- 每個花瓣在 下是不變的。換句話說,它被 對映到自身:
- 域 (拓撲圓盤) 包含
- 拋物週期點 p 在其邊界 (精確地在其根部,它是所有吸引花瓣和排斥花瓣的公共點 = Lea-Fatou 花的中心)
- 臨界點或其在另一側的 n=週期像 (僅小的?)
- 陷阱 捕獲任何趨向於拋物點的軌道[3]
- 包含在填充的 Julia 集的元件內的集合。拋物固定點的吸引花瓣包含在其吸引盆中
- "... 就該屬性而言,它最大。這個首選花瓣 P max 始終在其邊界上有一個或多個臨界點。"[4]
- "吸引花瓣是完全位於 Fatou 集中的解析曲線的內部,在固定點處具有正確的切線性質,並且被對映到其內部,透過對映的正確冪" Scott Sutherland
- "... 吸引花瓣是週期點周圍足夠小的圓盤中的一組點,它們的正向軌道在返回對映的冪下始終保留在圓盤內。" (W P Thurston: 關於迭代有理對映的幾何和動力學)
花瓣 關於 d-1 方向 是對稱的
在哪裡
- d 是 (待做)
- l 從 0 到 d-2
花瓣可以有不同的尺寸。
如果 ,那麼 Julia 集應該在 n 個方向上接近拋物週期點,在 n 個花瓣之間。 [5]
"用全純動力學的語言來說,人們會說你正在研究多項式在拋物線不動點 附近的動力學。透過一個簡單的線性變數變換,任何這樣的拋物線不動點的研究都可以簡化為對 的研究。然後你可以應用另一個變換 。因此,你被簡化為對 的研究。如果實部 $Re(w)$ 足夠大,你將得到 。這將給你你想要的東西(當你回到 z 變數時)。
區域 (對於較大的 )看起來像某種心形(在你的特定情況下)當你把它視覺化在 z 變數中(它被詩意地稱為吸引花瓣)。 Sylvain Bonnot[6]
構造花瓣
[edit | edit source]
陷阱引數
- 形狀
- 中心
- 大小
子週期分量的目標集
- 1 和 2 目標集可以是圓,拋物線不動點位於其邊界上(目標集位於分量內部)。
- 對於週期 3 及更高(p > 2),目標集是中心在拋物線不動點處的圓的三角形片段。
- 按週期劃分的分量的目標集
-
p=1 圓形
-
p=2 圓形
-
p>2。三角形。這裡目標集很窄,所以未定義點是可見的。
-
p = 11 的射線和臨界軌道
- 分量陷阱:三角形
- BDM 陷阱:三角形
在哪裡
- z1、z2 是邊界分量的外部射線的最後一點(通常是最大的一個,臨界點在其中)。
- 是臨界點,或者如果臨界軌道臂不是直線,則它是它的前向像。
- 是拋物線不動點。
- 是一個前臨界點 = 臨界點的原像。
由於動力學延遲,計算在臨界軌道和外部射線落在拋物線不動點之前停止。剩餘的間隙用從最後一點到著陸點的線填充(近似)。
-
計算和近似部分
0/1 或 1/1
[edit | edit source]-
它是 fc(z)=z^2 + 1/4 的動態平面。它是圍繞拋物線不動點 z=0.5 的縮放。顯示了 Julia 集內部某些點的軌道(白色點)。
-
吸引花瓣(灰色)
-
拋物線不動點附近的動力學
-
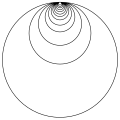
1 花瓣花(偶極子)內部動力學的連續模型
第一個吸引花瓣是一個圓,它具有
- 中心位於 x 軸上
- 半徑 = (cabs(zf) + cabs(z))/2
其他(更大的)吸引花瓣是第一個花瓣的前像,其中包括第一個花瓣。
在哪裡
- z 是臨界軌道的最後一點。
- zf 是一個不動點。
1/2
[edit | edit source]-
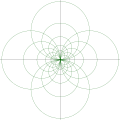
2 花瓣花(四極子)內部動力學的模型
-
點狀四極子場的等勢面的等高線圖
圓形吸引花瓣
- 中心位於定點和臨界點之間。
- 半徑小於定點和臨界點之間距離的一半。
// choose such value that level sets cross at z=0
// choose radius such a
double GivePetalRadius(complex double c, complex double fixed, int n){
complex double z = 0.0; // critical point
int k;
// best for n>1
int kMax = (n*ChildPeriod) - 1; // ????
for(k=0; k<kMax-1; ++k)
z = z*z + c; // forward iteration
return cabs(z-fixed)/2.0;
}
1/3
[edit | edit source]-
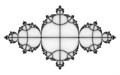
胖杜瓦迪兔子朱利亞集的定點附近的軌道
斯科特·薩瑟蘭的方法:[7]
- 選擇包含臨界點的連通分量
- 找到一條完全位於法圖集內的解析曲線,在定點處具有正確的切線性質,並且被對映到其內部的正確對映冪次
- 另外兩個只是這條曲線在第一次和第二次迭代下的影像。
其他情況
[edit | edit source]-
1/30
花瓣數量
[edit | edit source]| 此頁面上次編輯於 18 個月前,可能已被棄用 此頁面自 2023 年 3 月 18 日起未被編輯,但本書中的其他頁面可能已被編輯。檢視相關更改以檢視本書的當前狀態。 您可以透過編輯和更新本書來提供幫助。如果此頁面沒有被積極編輯,請刪除 {{under construction}}。在WB:PROJECTS中尋求幫助。 |

對於二次多項式
重數 = 父週期 + 子週期
花瓣數量 = 重數 - 父週期
這是因為在拋物情況下,定點與週期迴圈重合。迴圈的長度(子週期)等於花瓣的數量。
對於其他多項式對映
-
一個臨界點和 5 個花瓣
-
13 個臨界點和 26 個花瓣。
-
14 個臨界點和 14 個花瓣。
-
z^4-z 有 3 個臨界點和 6 個花瓣
| f(z) | 花瓣數量 | 解釋 |
|---|---|---|
| d-1 | 對於 點 z=0 的重數為 d | |
| d+2 | (?)對於 根 z=0 的重數為 d+3 | |
對於 f(z)= -z+z^(p+1) 拋物花具有
- 2p 個花瓣,當 p 為奇數時
- p 個花瓣,當 p 為偶數時[8]
... (待辦事項)