小學幾何/邊邊邊全等定理

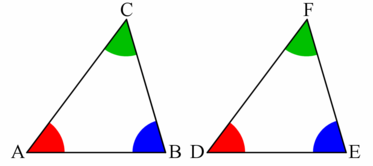
我們將要討論的第一個全等定理是邊邊邊定理。

邊邊邊全等定理

給定兩個三角形$\triangle ABC$ 和 $\triangle DEF$ 使得它們的邊相等，因此

1. 邊 ${\overline {AB}}$ 等於 ${\overline {DE}}$。
   
   
   
   
2. 邊 ${\overline {BC}}$ 等於 ${\overline {EF}}$。
   
   
   
   
3. 邊 ${\overline {AC}}$ 等於 ${\overline {DF}}$。
   
   
   
   

那麼這兩個三角形全等，它們的角也相等。

證明方法

為了證明這個定理，我們需要一個新的公設。這個公設是，可以在平面上移動或翻轉任何形狀，而不會改變它。特別地，可以移動三角形而不改變它的邊或角。請注意，這個公設在平面幾何中是成立的，但在一般情況下不成立。如果考慮球體上的幾何，這個公設就不再成立了。

給定這個公設，我們將展示如何將一個三角形移動到另一個三角形的位置，並表明它們重合。因此，這兩個三角形是相等的。

構造

1. 複製線段 邊 ${\overline {AB}}$ 到點 D。
2. 畫圓 $\circ D,{\overline {AB}}$。
3. 圓 $\circ D,{\overline {AB}}$ 和 線段 ${\overline {DE}}$ 相交於點 E，因此我們有了 ${\overline {AB}}$ 的副本，使它與 ${\overline {DE}}$ 重合。
4. 構造一個三角形，以 ${\overline {DE}}$ 為底，${\overline {BC}}$，${\overline {AC}}$ 為邊，頂點在頂點 F 的同一側。把這個三角形稱為三角形 $\triangle DEG$

斷言

三角形 $\triangle DEF$ 和 $\triangle ABC$ 全等。

證明

1. 點 A 和 D 重合。
2. 點 B 和 E 重合。
3. 頂點 F 是 $\circ D,{\overline {DF}}$ 和 $\circ E,{\overline {EF}}$ 的交點。
4. 頂點 G 是 $\circ D,{\overline {AC}}$ 和 $\circ E,{\overline {BC}}$ 的交點。
5. 已知 ${\overline {DF}}$ 等於 ${\overline {AC}}$.
6. 已知 ${\overline {EF}}$ 等於 ${\overline {BC}}$.
7. 因此，$\circ D,{\overline {DF}}$ 等於 $\circ D,{\overline {AC}}$，並且 $\circ E,{\overline {EF}}$ 等於 $\circ E,{\overline {BC}}$。
8. 然而，不同圓心的圓在連線其圓心的線段一側最多隻有一個交點。
9. 因此，點 G 和 F 重合。
10. 兩點之間只有一條直線，因此 ${\overline {EG}}$ 與 ${\overline {EF}}$ 重合，並且 ${\overline {GD}}$ 與 ${\overline {DF}}$ 重合。
11. 因此，$\triangle DEG$ 與 $\triangle DEF$ 重合，兩者全等。
12. 根據公設，$\triangle DEG$ 和 $\triangle ABC$ 相等，因此全等。
13. 因此，$\triangle DEF$ 和 $\triangle ABC$ 全等。
14. 因此，$\angle ABC$ 等於 $\angle DEF$，$\angle BCA$ 等於 $\angle EFD$ 以及 $\angle CAB$ 等於 $\angle FDE$.

注意

邊邊邊全等定理出現在歐幾里得幾何《原本》的第 I 卷，命題 8 中。這裡的證明遵循了歐幾里得最初證明的思路。在最初的證明中，歐幾里得認為頂點 **F** 和 **G** 必須重合，但並沒有說明為什麼。我們使用了這樣的假設：“不同圓心的圓在連線圓心的線段的一側最多有一個交點”。這個假設在平面幾何中是正確的，但不能從歐幾里得最初的公理推匯出來。由於歐幾里得自己需要使用這樣的假設，我們更傾向於給出一個更詳細的證明，儘管多出了一個假設。