波/向量

波 : 二維和三維波
1 - 2 - 3 - 4 - 5 - 6 - 7
問題

數學教程--向量

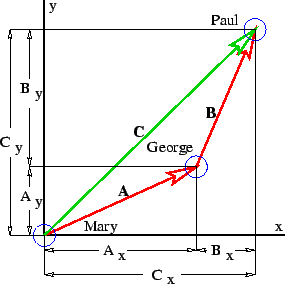
圖 1: 平面上的位移向量。
向量 ${\mbox{A}}$ 表示喬治相對於瑪麗的位移，而向量 ${\mbox{B}}$ 表示保羅相對於喬治的位移。向量 ${\mbox{C}}$ 表示保羅相對於瑪麗的位移，並且 ${\mbox{C}}={\mbox{A}}+{\mbox{B}}$。數量 $A_{x}$，$A_{y}$，等等，表示這些向量在笛卡爾座標系下的分量。

在我們繼續之前，我們需要了解一下向量的概念。向量是一個既表示大小又表示方向的量。在圖形上，我們用箭頭來表示向量。在排版中，向量用粗體字元表示，而在手寫中，在代表向量的字元上畫一個箭頭。

圖 1 展示了一些位移向量的示例，即表示一個物體相對於另一個物體的位移的向量，並引入了向量加法的概念。向量 ${\mbox{B}}$ 的尾部與向量 ${\mbox{A}}$ 的頭部重合，從 ${\mbox{A}}$ 的尾部延伸到 ${\mbox{B}}$ 的頭部的向量是 ${\mbox{A}}$ 和 ${\mbox{B}}$ 的和，在圖 1 中稱為 ${\mbox{C}}$。

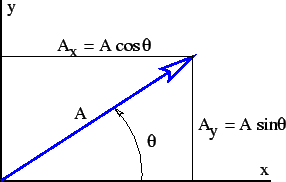
圖 2: 用於表示二維向量方向的角度 $\theta$ 的定義草圖。

數量 $A_{x}$，$A_{y}$，等等，表示圖 2 中向量在笛卡爾座標系下的分量。向量可以用它的笛卡爾座標系分量來表示，這些分量只是向量在笛卡爾座標系軸上的投影，也可以用它的方向和大小來表示。二維向量方向通常用向量相對於 $x$ 軸的逆時針角度表示，如圖 2 所示。從一種形式到另一種形式的轉換由以下方程式給出

$A=(A_{x}^{2}+A_{y}^{2})^{1/2}\qquad \theta =\tan ^{-1}(A_{y}/A_{x}),$

$A_{x}=A\cos(\theta )\qquad A_{y}=A\sin(\theta ),$

其中$A$ 是向量的長度。向量長度有時用絕對值符號表示：$A\equiv \vert {\mbox{A}}\vert$.

需要注意的是，反正切函式的結果對於加減整數倍的$\pi$ 是不確定的。因此，必須透過獨立檢查$A_{x}$ 和$A_{y}$ 的符號來確定角度所在的象限，並選擇相應的$\theta$ 值。

要將兩個向量${\mbox{A}}$ 和 ${\mbox{B}}$ 相加，最簡單的方法是將它們轉換為笛卡爾座標形式。和向量${\mbox{C}}={\mbox{A}}+{\mbox{B}}$ 的分量就等於它們各自分量的和

$C_{x}=A_{x}+B_{x}\qquad C_{y}=A_{y}+B_{y}.$

向量減法類似進行，例如，如果${\mbox{A}}={\mbox{C}}-{\mbox{B}}$，那麼

$A_{x}=C_{x}-B_{x}\qquad A_{y}=C_{y}-B_{y}.$

單位向量是指長度為 1 的向量。可以透過將普通向量除以其長度來構造單位向量：${\mbox{n}}={\mbox{A}}/\vert {\mbox{A}}\vert$。 此除法操作是透過將向量中的每個分量除以分母中的數字來執行的。 或者，如果向量用長度和方向表示，則將向量的模除以分母，方向不變。

單位向量可用於定義笛卡爾座標系。 通常，${\mbox{i}}$，${\mbox{j}}$ 和 ${\mbox{k}}$ 分別表示該系統中的 $x$，$y$ 和 $z$ 軸。 注意 ${\mbox{i}}$，${\mbox{j}}$ 和 ${\mbox{k}}$ 互相垂直。 任何向量都可以用單位向量及其笛卡爾分量表示：${\mbox{A}}=A_{x}{\mbox{i}}+A_{y}{\mbox{j}}+A_{z}{\mbox{k}}$。 表示向量的另一種方法是作為分量列表：${\mbox{A}}=(A_{x},A_{y},A_{z})$。 我們傾向於使用後一種表示，因為它在某種程度上是一種更經濟的表示法。

有兩種方法可以將兩個向量相乘，分別得到稱為點積和叉積的結果。 叉積得到另一個向量，而點積得到一個數字。 在這裡，我們將只討論點積。

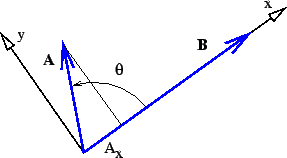圖 3：點積定義示意圖。

給定向量 ${\mbox{A}}$ 和 ${\mbox{B}}$，這兩個向量的點積定義為

${\mbox{A}}\cdot {\mbox{B}}\equiv \vert {\mbox{A}}\vert \vert {\mbox{B}}\vert \cos \theta ,$

其中 $\theta$ 是兩個向量之間的夾角。點積的另一種表示式以向量的笛卡爾座標表示

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}.$

很容易證明，當 $x$ 軸沿其中一個向量，如圖 3 所示，這等同於點積的餘弦形式。特別要注意，$A_{x}=\vert {\mbox{A}}\vert \cos \theta$，而 $B_{x}=\vert {\mbox{B}}\vert$ 和 $B_{y}=0$。因此，${\mbox{A}}\cdot {\mbox{B}}=\vert {\mbox{A}}\vert \cos \theta \vert {\mbox{B}}\vert$在這種情況下，這與上面給出的形式相同。

根據餘弦定理，我們還可以看到

$\mathbf {A} \cdot \mathbf {B} ={\frac {1}{2}}\left(|\mathbf {A} +\mathbf {B} |^{2}-|\mathbf {A} |^{2}-|\mathbf {B} |^{2}\right)$

這是一個點積的另一種無座標表示式。

圖 4：旋轉座標系的定義圖。向量 ${\mbox{R}}$ 在非標註座標系中的分量為 $X$ 和 $Y$，在標註座標系中的分量為 $X'$ 和 $Y'$。

要證明方程 (2.6) 通常成立，剩下的就是證明無論笛卡爾座標系相對於向量如何定向，它都能得到相同的結果。為此，我們必須證明 $A_{x}B_{x}+A_{y}B_{y}=A_{x}'B_{x}'+A_{y}'B_{y}'$，其中撇號表示從原始座標系旋轉的座標系中的分量。

這可以透過應用勾股定理幾乎立即證明。由於 R 是不變的，並且代表兩個三角形 (X, X', Y 和 Y') 的斜邊，我們可以得出結論

$|R|^{2}=X^{2}+Y^{2}{\mbox{ and }}|R|^{2}=X'^{2}+Y'^{2}\Rightarrow X^{2}+Y^{2}=X'^{2}+Y'^{2}$

由於點積可以像上面那樣完全用幅度表示，如果向量的幅度保持不變，則兩個向量的點積也必須保持不變。

要推匯出 X' 和 Y' 的一般公式，你需要多思考一下。

圖 2.4 顯示了向量 ${\mbox{R}}$ 在兩個相互旋轉的座標系中分解。從圖中可以清楚地看出，$X'=A+B$。專注於陰影三角形，我們看到 $A=X\cos \theta$ 和 $B=Y\sin \theta$。因此，我們得到 $X'=X\cos \theta +Y\sin \theta$。類似的推理表明 $Y'=-X\sin \theta +Y\cos \theta$（只需想象將影像中的構造體再旋轉 90°，但不改變軸名稱。你就會立即注意到，在第二象限中 X 為負而 Y 為正）。

因此，新座標和舊座標的關係是

${\begin{pmatrix}X^{\prime }\\Y^{\prime }\end{pmatrix}}={\begin{pmatrix}X\cos \theta +Y\sin \theta \\-X\sin \theta +Y\cos \theta \end{pmatrix}}$

這適用於位置向量。我們可以利用它將向量概念擴充套件到位置以外的概念，方法是宣告，一對數字是向量，當且僅當它在旋轉下以這種方式變化。

將此關係代入我們之前對點積的表示式，並使用三角恆等式 $\cos ^{2}\theta +\sin ^{2}\theta =1$，得到

${\begin{matrix}A_{x}'B_{x}'+A_{y}'B_{y}'&=&&(A_{x}\cos \theta +A_{y}\sin \theta )(B_{x}\cos \theta +B_{y}\sin \theta )\\&&+&(-A_{x}\sin \theta +A_{y}\cos \theta )(-B_{x}\sin \theta +B_{y}\cos \theta )\\&=&&A_{x}B_{x}+A_{y}B_{y}\end{matrix}}$

這證明了上面引用的兩種點積形式的完全等效性。（展開上面的表示式來驗證這一點。）

不依賴於所使用座標系的數值稱為標量。兩個向量的點積是一個標量。然而，向量的分量，單獨考慮，不是標量，因為分量會隨著座標系的改變而改變。由於物理定律不能依賴於所使用座標系的選擇，我們堅持認為物理定律應該用標量和向量來表示，但不能用向量的分量來表示。

在三維空間中，點積的餘弦形式保持不變，而分量形式是

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}.$