波/向量

波 : 二維和三維波
1 - 2 - 3 - 4 - 5 - 6 - 7
問題

數學教程 - 向量

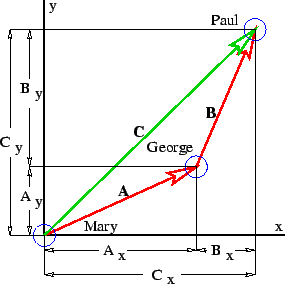
圖 1: 平面中的位移向量。
向量 ${\mbox{A}}$ 代表喬治從瑪麗的位移，而向量 ${\mbox{B}}$ 代表保羅從喬治的位移。向量 ${\mbox{C}}$ 代表保羅從瑪麗的位移，並且 ${\mbox{C}}={\mbox{A}}+{\mbox{B}}$。量 $A_{x}$，$A_{y}$ 等，代表向量的笛卡爾座標。

在我們繼續之前，我們需要探索向量的概念。向量是一個表示大小和方向的量。在圖形上，我們將向量表示為箭頭。在排版符號中，向量用粗體字表示，而在手寫中，在表示向量的字元上畫一個箭頭。

圖 1 展示了一些位移向量的例子，即表示一個物體相對於另一個物體的位移的向量，並介紹了向量加法的概念。向量 ${\mbox{B}}$ 的尾部與向量 ${\mbox{A}}$ 的頭部重合，連線 ${\mbox{A}}$ 尾部和 ${\mbox{B}}$ 頭部的向量是 ${\mbox{A}}$ 和 ${\mbox{B}}$ 的和，在圖 1 中稱為 ${\mbox{C}}$。

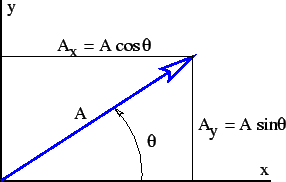
圖 2: 用於表示二維向量方向的角 $\theta$ 的定義草圖。

量 $A_{x}$，$A_{y}$等，代表圖2中向量的笛卡爾座標分量。一個向量可以用它的笛卡爾座標分量來表示，笛卡爾座標分量只是向量在笛卡爾座標軸上的投影，也可以用它的方向和大小來表示。二維向量的方向通常用向量相對於 $x$ 軸的逆時針角度來表示，如圖2所示。從一種形式到另一種形式的轉換由以下公式給出。

$A=(A_{x}^{2}+A_{y}^{2})^{1/2}\qquad \theta =\tan ^{-1}(A_{y}/A_{x}),$

$A_{x}=A\cos(\theta )\qquad A_{y}=A\sin(\theta ),$

其中 $A$ 是向量的大小。向量大小有時用絕對值符號表示：$A\equiv \vert {\mbox{A}}\vert$。

請注意，反正切函式給出的結果對於新增或減去 $\pi$ 的整數倍是不確定的。因此，必須透過獨立檢查 $A_{x}$ 和 $A_{y}$ 的符號來確定角度所在的象限，並選擇 $\theta$ 的適當值。

要將兩個向量 ${\mbox{A}}$ 和 ${\mbox{B}}$ 相加，最簡單的方法是將它們轉換為笛卡爾座標分量形式。然後，和 ${\mbox{C}}={\mbox{A}}+{\mbox{B}}$ 的分量只是分量的和。

$C_{x}=A_{x}+B_{x}\qquad C_{y}=A_{y}+B_{y}.$

向量的減法類似地完成，例如，如果 ${\mbox{A}}={\mbox{C}}-{\mbox{B}}$，則

$A_{x}=C_{x}-B_{x}\qquad A_{y}=C_{y}-B_{y}.$

單位向量是一個長度為1的向量。可以透過將普通向量除以其長度來構造一個單位向量：${\mbox{n}}={\mbox{A}}/\vert {\mbox{A}}\vert$。該除法運算透過將每個向量分量除以分母中的數字來執行。或者，如果向量以長度和方向表示，則向量的幅值除以分母，方向保持不變。

單位向量可用於定義笛卡爾座標系。按照慣例，${\mbox{i}}$，${\mbox{j}}$，和${\mbox{k}}$分別指示該系統的$x$，$y$，和$z$軸。請注意，${\mbox{i}}$，${\mbox{j}}$，和${\mbox{k}}$是相互垂直的。任何向量都可以用單位向量及其笛卡爾分量表示：${\mbox{A}}=A_{x}{\mbox{i}}+A_{y}{\mbox{j}}+A_{z}{\mbox{k}}$。表示向量的另一種方法是作為分量列表：${\mbox{A}}=(A_{x},A_{y},A_{z})$。我們傾向於使用後一種表示，因為它是一種比較簡潔的符號。

有兩種方法可以將兩個向量相乘，分別產生稱為點積和叉積的結果。叉積產生另一個向量，而點積產生一個數字。這裡我們將只討論點積。

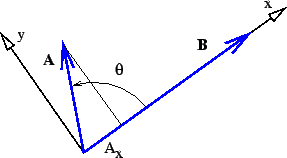圖 3: 點積的定義草圖。

給定向量 ${\mbox{A}}$ 和 ${\mbox{B}}$，這兩個向量的點積定義為

${\mbox{A}}\cdot {\mbox{B}}\equiv \vert {\mbox{A}}\vert \vert {\mbox{B}}\vert \cos \theta ,$

其中 $\theta$ 是這兩個向量之間的夾角。點積的另一種表示式用向量笛卡爾座標表示

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}.$

很容易證明當 $x$ 軸沿著其中一個向量時，這與點積的餘弦形式是等效的，如圖 3 所示。特別要注意，$A_{x}=\vert {\mbox{A}}\vert \cos \theta$，而 $B_{x}=\vert {\mbox{B}}\vert$ 和 $B_{y}=0$。因此，${\mbox{A}}\cdot {\mbox{B}}=\vert {\mbox{A}}\vert \cos \theta \vert {\mbox{B}}\vert$，在這種情況下，這與上面給出的形式相同。

根據餘弦定律，我們也可以看到

$\mathbf {A} \cdot \mathbf {B} ={\frac {1}{2}}\left(|\mathbf {A} +\mathbf {B} |^{2}-|\mathbf {A} |^{2}-|\mathbf {B} |^{2}\right)$

這是點積的另一種無座標表示式。

圖 4：旋轉座標系的定義圖。向量 ${\mbox{R}}$ 在未加撇的座標系中具有分量 $X$ 和 $Y$，在加撇的座標系中具有分量 $X'$ 和 $Y'$。

為了使方程式 (2.6) 一般情況下成立，剩下的唯一需要證明的就是無論笛卡爾座標系相對於向量的方向如何，它都能得出相同的結果。為此，我們必須證明 $A_{x}B_{x}+A_{y}B_{y}=A_{x}'B_{x}'+A_{y}'B_{y}'$，其中撇號表示旋轉後的座標系中的分量。

這可以透過應用勾股定理幾乎立即證明。由於 R 是不變的，並且代表兩個三角形（X, X', Y 和 Y'）的斜邊，我們可以得出結論

$|R|^{2}=X^{2}+Y^{2}{\mbox{ and }}|R|^{2}=X'^{2}+Y'^{2}\Rightarrow X^{2}+Y^{2}=X'^{2}+Y'^{2}$

由於點積可以像上面一樣僅用大小來表示，如果向量的模是不變的，那麼兩個向量的點積也必須是不變的。

要推匯出 X' 和 Y' 的一般公式，你需要多思考一些

圖 2.4 顯示了向量 ${\mbox{R}}$ 在兩個相互旋轉的座標系中分解。從該圖可以清楚地看出 $X'=A+B$。聚焦於陰影三角形，我們可以看到 $A=X\cos \theta$ 和 $B=Y\sin \theta$。因此，我們發現 $X'=X\cos \theta +Y\sin \theta$。類似的推理表明 $Y'=-X\sin \theta +Y\cos \theta$（想象一下，在不改變軸名稱的情況下，將影像中的結構再旋轉 90°。你會立即注意到，在第二象限中，X 為負而 Y 為正）。

因此，新舊座標的關係為

${\begin{pmatrix}X^{\prime }\\Y^{\prime }\end{pmatrix}}={\begin{pmatrix}X\cos \theta +Y\sin \theta \\-X\sin \theta +Y\cos \theta \end{pmatrix}}$

這對位置向量是成立的。我們可以用它來擴充套件向量概念，使其不僅限於位置，而是宣告一對數字是向量，當且僅當它們的值在旋轉下以這種方式變化。

將此關係代入我們之前點積的表示式，並使用三角恆等式 $\cos ^{2}\theta +\sin ^{2}\theta =1$，得到

${\begin{matrix}A_{x}'B_{x}'+A_{y}'B_{y}'&=&&(A_{x}\cos \theta +A_{y}\sin \theta )(B_{x}\cos \theta +B_{y}\sin \theta )\\&&+&(-A_{x}\sin \theta +A_{y}\cos \theta )(-B_{x}\sin \theta +B_{y}\cos \theta )\\&=&&A_{x}B_{x}+A_{y}B_{y}\end{matrix}}$

這證明了上面提到的兩種點積形式的完全等價性。(展開上面的表示式以驗證這一點。)

一個不依賴於使用哪個座標系的數量被稱為標量。兩個向量的點積是一個標量。然而，單獨取的向量的分量不是標量，因為分量隨著座標系的改變而改變。由於物理定律不能依賴於使用的座標系的選擇，我們堅持要求物理定律用標量和向量來表示，而不是用向量的分量來表示。

在三維空間中，點積的餘弦形式保持不變，而分量形式為

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}.$