波/平面疊加

波 : 二維和三維波
1 - 2 - 3 - 4 - 5 - 6 - 7
問題

平面波的疊加

我們現在透過詢問兩個平面正弦波疊加後的樣子來研究二維波包。 如果這兩個波具有不同的波數，但它們的波向量指向同一個方向，則結果與前一章中介紹的結果相同，只是波包在垂直於波向量的方向上無限延伸而不改變形狀。在這種情況下產生的波包沿著波向量的方向前進，因此對於靜止的觀察者來說，就像一系列寬闊橫向範圍的經過的脈衝。

疊加兩個具有相同頻率的平面波會導致一個靜止的波包，單個波前透過該波包。 該波包也在某個方向上無限延伸，但延伸方向取決於所考慮波的色散關係。人們可以將這種波包視為穩定的光束，它引導某個方向的單個相位波，但它們本身不會隨時間變化。透過疊加多個平面波，所有平面波都具有相同的頻率，實際上可以產生一個靜止的光束，就像可以透過疊加多個具有指向相同方向的波向量的波來產生一個孤立的脈衝一樣。

兩個相同波長的波

如果波的頻率取決於波向量的大小，但不取決於它的方向，則該波的色散關係稱為各向同性。 在各向同性的情況下，只有當兩個波的波向量長度，因此它們的波長相同，兩個波的頻率才相同。 圖 2.6 中的前兩個示例滿足此條件。在本節中，我們研究由疊加的各向同性波產生的光束。

我們疊加兩個平面波，其波向量分別為${\mbox{k}}_{1}=(-\Delta k_{x},k_{y})$ 和 ${\mbox{k}}_{2}=(\Delta k_{x},k_{y})$。兩種情況下的波向量長度均為 $k_{1}=k_{2}=(\Delta k_{x}^{2}+k_{y}^{2})^{1/2}$

$A=\sin(-\Delta k_{x}x+k_{y}y-\omega t)+\sin(\Delta k_{x}x+k_{y}y-\omega t).$ (3.15)

如果 $\Delta k_{x}<<k_{y}$，則兩個波都近似地在 $y$ 方向移動。這種波的一個例子是兩個具有相同頻率但以略微不同的方向移動的光波。

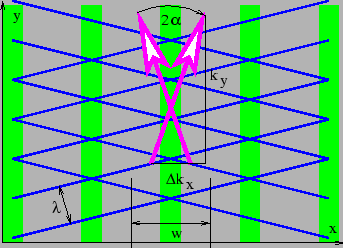圖 2.7：兩個具有相同波長但以不同方向定向的平面波的波前和波向量。 垂直條帶顯示了波前重合的干涉相長區域。條帶之間的垂直區域發生了干涉相消，因此定義了疊加產生的光束的橫向邊界。波向量的一個分量$\Delta k_{x}$ 和 $k_{y}$ 如圖所示。

應用兩個角度之和的正弦的三角恆等式（正如我們之前所做的那樣），方程式 (3.15) 可以簡化為

$A=2\sin(k_{y}y-\omega t)\cos(\Delta k_{x}x).$ (3.16)

這是一種在$y$方向上以相速度$c_{phase}=\omega /k_{y}$和波數$k_{y}$傳播的正弦波形式，在$x$方向上被餘弦函式調製。$x$方向上破壞性干涉區域之間的距離$w$告訴我們所產生光束的寬度，它由$\Delta k_{x}w=\pi$給出，因此

$w=\pi /\Delta k_{x}.$ (3.17)

因此，$\Delta k_{x}$越小，光束直徑越大。這種行為在圖 2.7 中得到了說明。

圖 2.8：兩個相同波長但傳播方向不同的平面波產生的光束示例。這兩個波的波矢為${\mbox{k}}=(\pm 0.1,1.0)$。正位移區域用垂直陰影線表示，負位移區域用水平陰影線表示。

圖 2.8 展示了兩個相同波長的平面波疊加產生的光束示例，它們的方向與圖 2.7 中所示相同。很容易證明所得到的波包的橫向寬度滿足公式 (2.17)。

兩個不同波長的波

在圖 2.6 的第三個示例中，波的頻率僅取決於波矢的方向，與它的幅值無關，這與各向同性色散關係正好相反。在這種情況下，不同方向但頻率相同的平面波具有相同方向但長度不同的波矢。

更一般地說，人們可能會遇到頻率依賴於波矢方向和幅值的波。在這種情況下，兩個不同方向但頻率相同的平面波通常具有方向和幅值都不同的波矢。

圖 2.9：兩個不同波長且方向不同的平面波的波前和波矢。傾斜的條帶顯示了波前重合的相長干涉區域。條帶之間的傾斜區域發生相消干涉，並且如前所述，定義了疊加產生的光束的橫向極限。

數學上，我們可以將這兩個波的疊加表示為公式 (2.15) 的推廣

$A=\sin[-\Delta k_{x}x+(k_{y}+\Delta k_{y})y-\omega t]+\sin[\Delta k_{x}x+(k_{y}-\Delta k_{y})y-\omega t].$ (3.18)

在這個方程中，我們給出了第一個波矢的 y 方向分量 $y$ 為 $k_{y}+\Delta k_{y}$，而第二個波矢的 y 方向分量為 $k_{y}-\Delta k_{y}$。因此，第一個波的總波數為 $k_{1}=[\Delta k_{x}^{2}+(k_{y}+\Delta k_{y})^{2}]^{1/2}$，而第二個波的總波數為 $k_{2}=[\Delta k_{x}^{2}+(k_{y}-\Delta k_{y})^{2}]^{1/2}$，因此 $k_{1}\neq k_{2}$。利用常用的三角恆等式，我們將方程 (2.18) 寫成：

$A=2\sin(k_{y}y-\omega t)\cos(-\Delta k_{x}x+\Delta k_{y}y).$ (3.19)

為了理解這個方程的含義，注意到當 $-\Delta k_{x}x+\Delta k_{y}y=m\pi$時，兩個波之間發生相長干涉，其中 $m$ 是一個整數。解這個方程關於 $y$，得到 $y=(\Delta k_{x}/\Delta k_{y})x+m\pi /\Delta k_{y}$，對應於斜率為 $\Delta k_{x}/\Delta k_{y}$ 的直線。這些直線垂直於兩個波矢的向量差 ${\mbox{k}}_{2}-{\mbox{k}}_{1}=(2\Delta k_{x},-2\Delta k_{y})$。證明這一點最簡單的方法是注意到，該差向量的方向是使它具有斜率 $-\Delta k_{y}/\Delta k_{x}$。與相長干涉直線的斜率 $\Delta k_{x}/\Delta k_{y}$ 相比，表明了這一點。

圖 2.10：兩個平面波產生波束的示例，這兩個平面波的波矢在方向和大小上都不同。這兩個波的波矢為 ${\mbox{k}}_{1}=(-0.1,1.0)$ 和 ${\mbox{k}}_{2}=(0.1,0.9)$。正位移區域用垂直陰影線表示，負位移區域用水平陰影線表示。

圖 2.10 展示了兩個方向和波長不同的波疊加產生波束的示例。注意，波前仍然是水平的，如 圖 2.8 所示，但波束不是垂直的，而是向右傾斜。

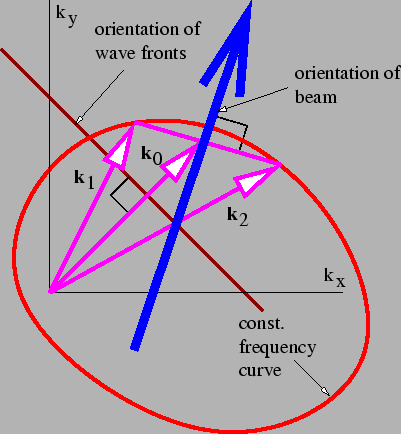圖 2.11：說明了兩個具有相同頻率的平面波疊加時所涉及的因素。波前垂直於兩個波矢的向量平均值 ${\mbox{k}}_{0}=({\mbox{k}}_{1}+{\mbox{k}}_{2})/2$，而定義波束方向的相長干涉線垂直於這兩個向量的差值 ${\mbox{k}}_{2}-{\mbox{k}}_{1}$。

圖 2.11 總結了我們對相同頻率的平面波疊加的瞭解。一般來說，波束方向和相長干涉線不垂直於波前。這種情況只發生在波頻率與波矢方向無關時。

多個具有相同波長的波

與一維波包類似，我們可以將兩個以上的波疊加在一起以產生一個孤立的波包。在這裡，我們將注意力集中在各向同性色散關係的情況下，其中給定頻率的所有波矢都具有相同的長度。

圖 2.12：說明了可以疊加在一起的平面波的波矢。

圖 2.12 展示了一個示例，其中將具有相同波長但方向不同的波矢疊加在一起。定義 $\alpha _{i}$ 為第 $i$ 個波矢從垂直方向順時針旋轉的角度，如圖 2.12 所示，我們可以將這些波在時間 $t=0$ 時的疊加寫成 $A=\sum _{i}A_{i}\sin(k_{xi}x+k_{yi}y)$

$=\sum _{i}A_{i}\sin[kx\sin(\alpha _{i})+ky\cos(\alpha _{i})]$ (3.20)

其中我們假設 $k_{xi}=k\sin(\alpha _{i})$ 和 $k_{yi}=k\cos(\alpha _{i})$。引數 $k=\vert {\mbox{k}}\vert$ 是波矢的大小，對於所有波來說都是相同的。在這個例子中，我們還假設每個波分量的幅度隨著 $\vert \alpha _{i}\vert$ 的增大而減小。

$A_{i}=\exp[-(\alpha _{i}/\alpha _{max})^{2}].$ (3.21)

指數函式隨著其自變數變為負而快速下降，出於實際目的，只有波矢滿足 $\vert \alpha _{i}\vert \leq \alpha _{max}$ 的波矢對總和有顯著貢獻。我們將 $\alpha _{max}$ 稱為 *擴充套件角*。

圖 2.13: 對於 $\alpha _{max}=0.8$ 和 $k=1$，公式 (2.20) 中的位移場 $A(x,y)$ 的圖。

圖 2.13 展示了當 $\alpha _{max}=0.8{\mbox{ radians}}$ 且 $k=1$ 時 $A(x,y)$ 的樣子。注意，對於 $y=0$，波幅只有在 $-4<x<4$ 的小範圍內才較大。然而，對於 $y>0$，波浪傳播成一個寬闊的半圓形圖案。

圖 2.14: 對於 $\alpha _{max}=0.2$ 和 $k=1$，公式 (2.20) 中的位移場 $A(x,y)$ 的圖。

圖 2.14 展示了當擴充套件角 $\alpha _{max}=0.2{\mbox{ radians}}$ 時計算出的 $A(x,y)$ 的圖案。在這種情況下，波幅在 $y=0$ 的更寬的 $x$ 範圍內都很大，大約為 $-12<x<12$。另一方面，與圖 2.13 相比，波浪的後續傳播要小得多。

我們得出結論，具有窄波矢分佈的平面波疊加，其中心波矢指向 $y$ 方向（如 2.14 圖所示），會產生一個最初在 $x$ 方向上很寬，但隨著 $y$ 增加其寬度只略微增加的光束。然而，具有更寬波矢分佈的平面波疊加（如 2.13 圖所示）會產生一個最初在 $x$ 方向上很窄，但隨著 $y$ 增加其寬度迅速增加的光束。

透過與本節開頭討論的兩個波疊加的結果進行比較，可以更好地理解擴充套件角 $\alpha _{max}$ 和光束初始寬度的關係。如公式 (2.17) 所示，較大的 $k_{x}$ 值，因此 $\alpha$，與波包在 $x$ 方向上的尺寸小有關，反之亦然。兩個波的疊加沒有捕捉到當許多波疊加時發生的後續光束擴散，但它確實導致了 $\alpha _{max}$（在兩個波的情況下只是 $\tan ^{-1}(k_{x}/k_{y})$）和光束初始寬度的粗略定量關係。如果我們對 $\alpha =\alpha _{max}$ 使用小角度近似，使得 $\alpha _{max}=\tan ^{-1}(k_{x}/k_{y})\approx k_{x}/k_{y}\approx k_{x}/k$，那麼 $k_{x}\approx k\alpha _{max}$，公式 (2.17) 可以寫成 $w=\pi /k_{x}\approx \pi /(k\alpha _{max})=\lambda /(2\alpha _{max})$。因此，我們可以從波的波長 $\lambda$ 和光束的初始寬度 $w$ 找到近似擴充套件角。

$\alpha _{max}\approx \lambda /(2d)\quad {\mbox{(single slit spreading angle)}}.$ (3.22)