波/2-3D 問題

波 : 2 維和 3 維波
1 - 2 - 3 - 4 - 5 - 6 - 7
問題

問題

點 A 在原點。點 B 距離 A $3{\mbox{ m}}$ $3{\mbox{ m}}$ ，相對於 $x$ $x$ 軸逆時針方向 $30^{\circ }$ $30^{\circ }$ 。點 C 距離 A $2{\mbox{ m}}$ $2{\mbox{ m}}$ ，相對於 $x$ $x$ 軸逆時針方向 $100^{\circ }$ $100^{\circ }$ 。
1. 求從 A 到 B 的向量 ${\mbox{D}}_{1}$ 和從 A 到 C 的向量 ${\mbox{D}}_{2}$ 的笛卡爾座標。
2. 求從 B 到 C 的向量 ${\mbox{D}}_{3}$ 的笛卡爾座標。
3. 求 ${\mbox{D}}_{3}$ 的方向和大小。
對於上一問題中的向量，分別使用點積的餘弦形式和笛卡爾形式求 ${\mbox{D}}_{1}\cdot {\mbox{D}}_{2}$ 。檢查兩個答案是否相同。
用圖形或其他方法證明 $\vert {\mbox{A}}+{\mbox{B}}\vert \neq \vert {\mbox{A}}\vert +\vert {\mbox{B}}\vert$ ，除非向量 ${\mbox{A}}$ 和 ${\mbox{B}}$ 平行。
在 $x$ $x$ - $y$ $y$ 平面上定義的波形由 $h=h_{0}\sin({\mbox{k}}\cdot {\mbox{x}})$ $h=h_{0}\sin({\mbox{k}}\cdot {\mbox{x}})$ 定義，其中 ${\mbox{k}}=(1,2){\mbox{ cm}}^{-1}$ ${\mbox{k}}=(1,2){\mbox{ cm}}^{-1}$ 。
1. 在一張方格紙上畫出 $x$ 和 $y$ 軸，然後繪製一條穿過原點並平行於向量 ${\mbox{k}}$ 的直線。
2. 在同一個圖上繪製由 ${\mbox{k}}\cdot {\mbox{x}}=k_{x}x+k_{y}y=0$ 、 ${\mbox{k}}\cdot {\mbox{x}}=\pi$ 和 ${\mbox{k}}\cdot {\mbox{x}}=2\pi$ 定義的直線。檢查這些直線是否垂直於 ${\mbox{k}}$ 。
兩個相同頻率 $\omega$ $\omega$ 的深海平面波，大約向東移動。然而，其中一個波向東偏了 $\beta$ $\beta$ 度北，另一個波向東偏了 $\beta$ $\beta$ 度南。
1. 確定這兩個波之間干涉加強線的方向。
2. 確定干涉加強線之間的間距。
圖 2.20 圖示了色散關係的示例，其中頻率是波矢幅度和方向的函式。
1. 對於三個波矢中的每一個，波的相速度是多少？提示：您可能需要透過圖形方法獲得每個波矢的長度。
2. 對於每個波矢，波前的方向是什麼？
3. 對於每個圖示的波矢，繪製另外兩個波矢，它們的平均值為圖示的波矢，並且它們的頂點位於相同的頻率等高線上。確定由疊加的平面波產生的干涉加強線的方向，對於每個波矢對，它們都是波矢。

Figure 2.20: Graphical representation of the dispersion relation for shallow water waves

圖 2.20：在

x

方向流動的河流中淺水波的色散關係的圖形表示。頻率的單位是赫茲，波數的單位是每米。

兩個重力波具有相同的頻率，但波長略有不同。
1. 如果一個波的方向角為 $\theta =\pi /4{\mbox{ radians}}$ ，另一個波的方向角是多少？（參見圖 2.6。）
2. 確定這兩個波之間干涉加強線的方向。
平面波入射到單縫上，在縫隙後散射出半形為 $\alpha$ 的光。如果整個裝置浸沒在折射率為 $n=1.5$ 的液體中，光的散射角將如何改變？(提示：回想一下透明介質中的折射率是真空中的光速與介質中的光速之比。此外，當光從真空進入透明介質時，光的頻率不變。因此，光的波長將如何改變？)
確定需要多少直徑的望遠鏡才能分辨出距離地球 $6{\mbox{ light years}}$ 的一顆恆星的 $2\times 10^{8}{\mbox{ km}}$ 的行星。(假設藍光，其波長為 $\lambda \approx 4\times 10^{-7}{\mbox{ m}}=400{\mbox{ nm}}$ 。此外，出於本題目的考慮，不用擔心兩者之間亮度的巨大差異。)
地球上的雷射發射器發出的雷射束被月球上的角反射器反射回地球。
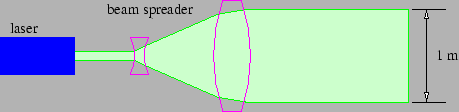
1. 工程師發現，如果雷射束最初由圖 2.21 所示的束擴束器擴散，則返回訊號更強。解釋一下為什麼是這樣。
2. 光束離開地球時的直徑為 $1{\mbox{ m}}$ 。它到達距離地球 $4\times 10^{5}{\mbox{ km}}$ 的月球時有多寬？假設光的波長為 $5\times 10^{-7}{\mbox{ m}}$ 。
3. 如果雷射束沒有最初透過束擴束器，它在月球上的寬度會是多少？假設其初始直徑為 $1{\mbox{ cm}}$ 。

Figure 2.21: Sketch of a beam expander for a laser

圖 2.21: 雷射束擴束器的示意圖。

假設平面波以一定角度照射到障礙物上的兩個縫隙，使得一個縫隙處的波相位滯後於另一個縫隙處的波相位半個波長。由此產生的干涉圖樣與沒有滯後情況下的干涉圖樣有何不同？
假設一塊折射率為 $n=1.33$ $n=1.33$ 的薄玻璃片放置在雙縫衍射裝置中一個縫隙的前面。
1. 玻璃片需要多厚才能使入射波減速，使其滯後於穿過另一個縫隙的波的相位差為 $\pi$ ？假設光的波長為 $\lambda =6\times 10^{-7}{\mbox{ m}}$ 。
2. 對於上述情況，描述一個縫隙前面沒有玻璃片的情況下的衍射圖樣是如何定性變化的。解釋你的結果。
一個光源發出兩種波長， $\lambda _{1}=400{\mbox{ nm}}$ $\lambda _{1}=400{\mbox{ nm}}$ （藍色）和 $\lambda _{2}=600{\mbox{ nm}}$ $\lambda _{2}=600{\mbox{ nm}}$ （紅色）。
1. 定性地描繪這個光源透過雙縫衍射產生的衍射圖樣。分別描繪每個波長的衍射圖樣。
2. 定性地描繪這個光源透過16縫衍射產生的衍射圖樣，其中縫間距與雙縫情況相同。
一個光源發出兩種波長， $\lambda _{1}=631{\mbox{ nm}}$ 和 $\lambda _{2}=635{\mbox{ nm}}$ 。為了區分這兩種波長，光柵光譜儀至少需要多少條狹縫？（假設觀察第一級衍射峰）。畫出每個波長的衍射峰，並標出為了區分它們，峰需要多窄。