波/雙縫衍射

波 : 二維和三維波
1 - 2 - 3 - 4 - 5 - 6 - 7
問題

兩條縫隙

窄縫

圖 2.16: 光線穿過縫隙 B 傳播到螢幕的距離比穿過縫隙 A 的光線多。該距離為 $\Delta l=d\sin \theta$

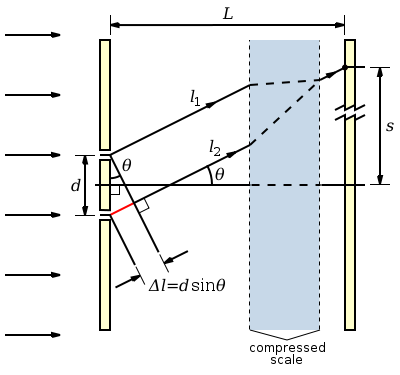
現在讓我們想象一個平面正弦波垂直入射到一個帶有兩個窄縫的螢幕上，這兩個窄縫的間距為d，如圖 2.16 所示。由於縫隙相對於入射波的波長很窄，光束的擴充套件角度很大，每個縫隙單獨產生的衍射圖樣都是一個向各個方向擴充套件的圓柱形波，如圖 2.13 所示。來自兩個縫隙的圓柱形波發生干涉，導致圖 2.16 右側螢幕上的波強度發生振盪。

當兩條光線的路徑長度差是波長λ的整數倍時，就會發生相長干涉。

[相長干涉條件]

$l_{2}-l_{1}=m\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

同樣，相消干涉發生在

[相消干涉條件]

$l_{2}-l_{1}=\left(m+{\frac {1}{2}}\right)\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

如果縫隙到螢幕的距離L遠大於縫隙間距d，則光線l₁和l₂近似平行，我們可以說路徑長度差為

[L >> d時的路徑長度差]

$l_{2}-l_{1}=d\sin \theta \,$

將這兩個等式代入得到以下相長干涉條件

[相長干涉條件]

$d\sin \theta =m\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

整數m稱為干涉級，表示兩條路徑差的波長數。在對應於整數m的每個角度上，相長干涉將最大，形成一個“條紋”。

螢幕上的一個點到中心線的距離s與θ的關係如下

$\tan \theta ={\frac {s}{L}}$

當θ很小時，我們可以說

$\tan \theta \approx \sin \theta$

因此我們可以將螢幕上的位置和條紋角度的表示式等同起來

${\frac {m\lambda }{d}}\approx {\frac {s}{L}}$

重新排列得到條紋間距的表示式

$s\approx {\frac {m\lambda L}{d}}$

要使此近似值有效，必須滿足以下條件

• 縫隙到螢幕的距離L必須遠大於縫隙間距d。
• 縫隙到條紋的角度θ必須很小。
• 縫隙必須比波長λ窄。

例子

讓我們考慮一個具有以下引數的設定

• d = 0.1 mm
• λ = 2500 nm（紅外線）

我們預計在 10 米處看到條紋間距為

$s={\frac {\lambda L}{d}}={\frac {2500\times 10^{-9}\times 10}{0.1\times 10^{-3}}}=0.25m$

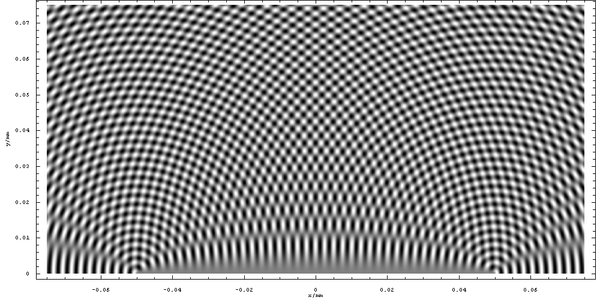
首先，讓我們看一下波在某個時刻的“快照”。點 (x,y) 的振幅由下式給出

$u(x,y,t)=a\sin \left(k{\sqrt {\left(x-{\frac {d}{2}}\right)^{2}+y^{2}}}\right)+a\sin \left(k{\sqrt {\left(x+{\frac {d}{2}}\right)^{2}+y^{2}}}\right)$

其中 k 是波數，由 2π/λ給出。在本練習中，我們將忽略隨著距離衰減的振幅，因此條紋在整個空間中都保持明亮。下圖顯示了該函式的圖。您可以清楚地看到每個光源的圓形傳播，但很難辨認出整體條紋結構。

現在，人眼和所有光測量裝置都沒有檢測到光波的單個振盪，它們測量的是強度。在這裡，強度是兩個光源之間相位差的函式，而相位差又與路徑長度差直接相關。

$\delta ={\frac {2\pi }{\lambda }}\Delta l$

$I\approx 4a^{2}\cos ^{2}{\frac {\delta }{2}}$

下圖顯示了該強度函式。我們看到一個非常清晰的條紋結構被揭示出來

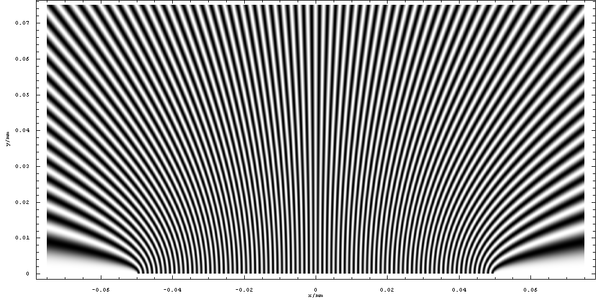
在這個尺度上，條紋結構不是明顯徑向的，它圍繞光源“彎曲”。但是，我們可以看到，如果我們放大，條紋會發散，而中心附近的條紋（最接近完全徑向的條紋）將是最重要的條紋

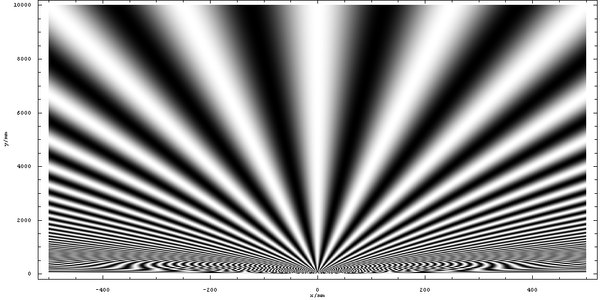
在這幅圖中，我們看到了預測的亮條紋，分別位於 x=0mm、x=±250mm 和 x=±500mm 處。

寬縫隙

雙寬縫實驗中的路徑長度差。