結合代數/導論

一個結合代數，或AC代數，(A, +, ×, *) 是一個結合代數 (A, +, ×) 同時也是一個合成代數 (A, *)。 就數學結構的公理而言，這些代數的特點是

$\forall a,b,c\in A\ \ (ab)c=a(bc),$ 以及

$\forall a,b\in A\ \ (ab)^{*}(ab)=(aa^{*})(bb^{*}).$

一個合成代數被構造為一個 域上的代數 F，並配備了一個對映 $N:\ A\rightarrow F\ \ {\text{by}}\ \ a\mapsto aa^{*}.$ 涉及共軛 (*) 的公理表達了 N 在 A 和 F 的乘法群之間 群同態 的性質。

結合代數分為三個層次：一元、二元和四元。 本文中的單元層次將是 R，實數，或 C，複數。 在單元層次上，共軛是恆等對映，以及 $N(a)=a^{2}$ 在這一級別。

這本書將描述另外五個結合代數：在 C 上只有一個二元和一個四元 AC 代數，但在 R 上卻有兩個。 後者中的兩個是除代數，並且有最多的文獻。 R 上的另外兩個是分裂合成代數；它們擁有零向量 $(aa^{*}=0).$

R 或 C 上的結合代數

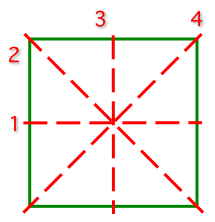正方形對稱軸上的反射會生成 8 階二面體群。

• R = 實數
• C = 除二元，也被稱為複數
• D = 分裂二元，也稱為分裂複數
• T = 雙二元，也稱為雙複數，也稱為四元數
• H = 除四元數，也稱為哈密頓實四元數
• Q = 分裂四元數，也稱為共四元數
• B = 雙四元數，也稱為復四元數

術語四元數和共四元數是由詹姆斯·考克爾在哲學雜誌中使用，是在哈密頓關於 H 和 B 的講座之後。 術語二元，是一個重要的語言插入，由凱文·麥克裡蒙在其著作約旦代數概覽（2004 年）中使用。

任何 AC 代數都可以為線性分數變換提供引數，這裡稱為射影變換，正如射影幾何中的傳統用法一樣。 演示從除二元的莫比烏斯變換和交叉比射影變換的構造開始。 三維運動學用四元數射影變換來表示。 用雙四元數射影變換來描述共形對映所表達的宇宙學對稱性。

在 AC 代數 A 中，$\ \{x\in A:x\ =\ x^{*}\}$ 是標量域，在本文中是 R 或 C。 在 R 的情況下，它是嵌入在 A 中的實數軸。 對於元素 $x\in A,\ \ (x+x^{*})/2$ 是x的標量部分，對於實代數來說，它是x的實部。

每個代數 A 在 $N(x+y)-N(x)-N(y)$ 上有一個雙線性形式，寫作

$\langle x,\ y\rangle \ :={\tfrac {1}{2}}(\ (xy^{*})+(x^{*}y)\ ).$

給定 $y\in A,\ \{x:\ \langle x,y\rangle \ =\ 0\}$ 是與 y 正交的元素集合，並且給定

$a,b\in A,\ \ \{x:(x-a)(x-a)^{*}=bb^{*}\}$ 是 A 中的二次集合。

透過莫比烏斯變換，以及在後面關於 射影變換 的章節中，將 A 嵌入其射影線中，這兩種型別的集合之間的區別將會減少。

以下引理使用複數 C 來準備解決問題 Q 的一種方法。

引理： 如果兩條直線以 θ 弧度傾斜，則這兩條直線上反射的合成是一個 2θ 弧度的旋轉。

代數證明：直線 L 和 M 相交於 X，X 取為 (0,0) ∈ C，其中 L 與實軸對齊。關於 L 的反射是複共軛。M 經過 $e^{i\theta }$（假設），關於 M 的反射透過將其旋轉到 L，然後共軛，最後旋轉回 L 的原始位置來實現。

$z\mapsto (e^{-i\theta }z)^{*}e^{i\theta }\ =\ e^{i\theta }z^{*}e^{i\theta }\ =\ e^{2i\theta }z^{*}.$

首先進行關於 L 的反射，$z\mapsto z^{*}.$ 然後關於 M 的反射是

$z^{*}\mapsto e^{2i\theta }z^{**}\ =\ e^{2i\theta }z.$ 合成是 $z\mapsto e^{2i\theta }z,$，一個旋轉角度是傾斜角的兩倍。