IIR 濾波器 通常基於連續時間濾波器函式 來設計。一旦選擇了傳遞函式,不同的濾波器結構允許實現濾波器,無論是在硬體中還是在軟體中。
經典的設計技術是從一個眾所周知的低通濾波器函式 開始,然後將其變換 為高通、帶通或帶阻函式(如果需要)。經典的傳遞函式是
傳遞函式 的一般形式由兩個多項式的比率給出

最直接的數字濾波器實現將透過實現其差分方程來完成,該方程由
![{\displaystyle y\left[k\right]=b_{0}x[k]+b_{1}x[k-1]+\cdots +b_{M}x[k-M]-a_{1}y[k-1]-a_{2}y[k-2]-\cdots -a_{N}y[k-N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fda4160d2142f0dbf6c2d8167c1b7c619daa7159)
以下電路顯示了 4 階濾波器差分方程的一種可能的實現方式
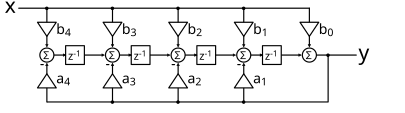 4 階典範 IIR 濾波器
4 階典範 IIR 濾波器
然而,這種形式在實踐中並不使用。事實上,第一個嘗試以這種方式實現濾波器的人發現該電路對係數值非常敏感:一個係數的微小變化可能會對濾波器傳遞函式的形狀產生巨大影響。因此,將係數舍入為整數或定點 值會導致設計噩夢。正因為如此,工程師轉向以下方法之一
- 模擬已被證明不會遭受這種嚴重敏感性的模擬濾波器結構
- 將總傳遞函式分解為二階段鏈,對於偶數階濾波器,再增加一個一階段
全極點濾波器 限於低通器件。它們沒有零點這一事實使其結構變得更加簡單。事實上,它們的傳遞函式寫成

一些基於模擬濾波器模擬的濾波器結構用於實現全極點濾波器。
巴特沃斯 和切比雪夫 I 型 函式都是全極點型別的。
帶有反饋的積分器鏈 (CIF) 允許對全極點傳遞函式進行直接實現。
 四階積分器鏈全極點濾波器
四階積分器鏈全極點濾波器
此電路,其中  到
到  是乘法器輸出,可以用以下方程描述
是乘法器輸出,可以用以下方程描述

這可以透過迭代求解來得到






從這個式子中,可以從傳遞函式的係數中迭代地獲取時間常數。
與模擬 CIF 相對應的數字結構在下圖中給出
 模擬積分器鏈的 4 階數字濾波器
模擬積分器鏈的 4 階數字濾波器
如果取樣率遠高於時間常數,則可以從模擬域的 CIF 直接獲取濾波器係數。否則,可以從取樣系統傳遞函式中找到它們

其中  .
.
跳蛙濾波器 模擬 模擬梯形濾波器 的功能,並提供了全極點傳遞函式的穩健實現。可以證明,係數值的很大變化只會導致傳遞函式的小變化,特別是在通帶內。
以以下 4 階全極點低通梯形濾波器為例,
 4 階集中元件梯形濾波器
4 階集中元件梯形濾波器
可以寫出以下方程

為了使左側只有電壓,重新編寫這些方程

這組新方程表明,該濾波器可以使用 4 個積分器鏈來實現,積分器具有以下形式的
- 狀態變數
 或
或 
- 時間常數 具有以下形式的
 或
或 
由此產生的電路是一個積分器鏈,其中每個積分器的輸出都回饋到前一個積分器的輸入。因此得名 leapfrog。

這種模擬裝置可以透過用累加器替換模擬積分器來實現數位電路。

濾波器係數可以從表格中得出,表格提供  、
、 和
和  為所選的 濾波器函式 和取樣週期
為所選的 濾波器函式 和取樣週期  的值。一個有趣的點是係數的相對值決定了傳遞函式的形狀 (巴特沃斯、切比雪夫 等),而它們的幅度決定了截止頻率。將所有係數除以 2 會使截止頻率降低一個倍頻程,這對應於 2 的因子。
的值。一個有趣的點是係數的相對值決定了傳遞函式的形狀 (巴特沃斯、切比雪夫 等),而它們的幅度決定了截止頻率。將所有係數除以 2 會使截止頻率降低一個倍頻程,這對應於 2 的因子。
需要注意的是,用累加器替換模擬積分器是一種非常原始的設計技術。在訊號處理方面,這對應於將 Z 變換簡化為  ,這是 泰勒級數 的前兩項
,這是 泰勒級數 的前兩項  。然而,對於取樣頻率遠高於訊號頻寬的濾波器,這種近似已經足夠好。
。然而,對於取樣頻率遠高於訊號頻寬的濾波器,這種近似已經足夠好。
上述濾波器的 狀態空間表示 可以寫成

從這個方程組中,我們可以寫出 A、B、C、D 矩陣為




有了這種表示,訊號處理工具,例如 SciPy、Octave 或 Matlab,就可以繪製濾波器的 頻率響應 或檢查其 零點和極點。
一個特例是 巴特沃斯 3 級濾波器,其時間常數具有 1、1/2 和 1 的相對值。因此,這種濾波器可以在硬體中實現,無需任何乘法器,而是使用移位運算。
帶有極點和零點的濾波器最適合以雙二次單元鏈的形式實現,或者透過兩個全通濾波器的並聯連線實現。
二階段,通常稱為雙二次,實現了一個二階傳遞函式。濾波器的傳遞函式可以拆分成一系列傳遞函式的乘積,每個傳遞函式都與一對極點和可能的一對零點相關聯。如果傳遞函式的階數是奇數,則必須在鏈中新增一個一階段。此部分與實極點和實零點(如果有)相關聯。
二階段的傳遞函式由下式給出

下面顯示了最常見的雙二次結構。
下圖顯示了直接形式 1 雙二次
 直接形式 1 雙二次
直接形式 1 雙二次
下圖顯示了直接形式 1 轉置雙二次
 直接形式 1 轉置雙二次
直接形式 1 轉置雙二次
下圖顯示了直接形式 2 雙二次
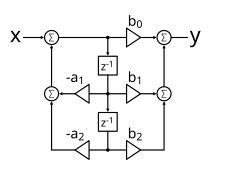 直接形式 2 雙二次
直接形式 2 雙二次
下圖顯示了直接形式 2 轉置雙二次
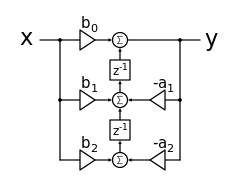 直接形式 2 轉置雙二次
直接形式 2 轉置雙二次
顯然,相應的一階段是透過去除係數  和
和  的乘法器以及相關的延遲元件來實現的。
的乘法器以及相關的延遲元件來實現的。
全通濾波器 用於修改訊號頻率分量的相位,而不改變其幅度。它們可用於補償其他不需要的相移,例如在設計接近線性相位的 IIR 濾波器時。
此外,兩個全通濾波器的並聯連線允許實現任何型別的傳遞函式。事實上,在兩個分支顯示相同相移的頻率處,輸出將跟隨輸入,但在相對相移為 180° 的頻率處,輸出將為零。此功能的一個例子是在數字波濾波器 (WDFs) 系列中給出的。











![{\displaystyle y\left[k\right]=b_{0}x[k]+b_{1}x[k-1]+\cdots +b_{M}x[k-M]-a_{1}y[k-1]-a_{2}y[k-2]-\cdots -a_{N}y[k-N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fda4160d2142f0dbf6c2d8167c1b7c619daa7159)
































