如何製作松木賽車/物理學

目錄

• 首頁
• 前言
• 規則
• 木塊
• 輪子
• 軸
• 組裝
• 物理學
• 附錄

編輯

本模組包含一些關於松木賽車的簡單物理學和一些化學知識。松木賽車將重力勢能轉換為平動動能（以及由此產生的速度）、旋轉動能（旋轉的輪子）和來自摩擦的熱量。最快的賽車是起始時重力勢能最大（重物在後部）、最終旋轉動能最小（輕質輪子，一個抬起）且摩擦損失能量最少的賽車（適當的潤滑和對準）。松木賽車是一個 5 盎司的實用物理學、化學和工程實驗室。

松木賽車問題在下面以兩種不同的方式進行處理：1）使用運動學方程；2）使用能量。這兩種方法都同樣有效，最終得到相同的結果。

運動學方程處理

我們將建立一個物理模型，考慮作用在松木賽車上的所有主要力。首先是重力，這是唯一（允許）的使賽車沿著斜坡加速的力。接下來，我們將考慮軸承對輪子的摩擦力和輪子踏板對軌道的摩擦力。最後，我們將考慮空氣阻力及其對賽車運動的影響。

在本節中，我們將考慮一個理想化的汽車和賽道。汽車的質量為*M*，為 5 盎司 (141.7 克)，長度為*l*，為 7 英寸，車輪的質量為*m*，為 2.6 克，半徑為*r*，為 0.5 英寸。賽道總長為*L*，由長度為 $L_{r}$ 的斜坡組成，斜坡的傾斜角度為 $\theta$，然後是一個長度為 $L_{f}$ 的水平路段，一直到終點。考慮到這種幾何形狀，起始高度的表示式為 $H=L_{r}\sin \theta$。為了簡化問題，我們暫時不會考慮斜坡與水平路段之間的過渡。典型的松木賽道賽車的引數值為 $L_{r}=$ 8 英尺 (2.44 米)，$L_{f}=$ 24 英尺 (7.32 米)，$H=$ 4 英尺 (1.22 米)，以及 $\theta$ = 30$^{\circ }$.

同時，考慮一個不受外力作用的物體的運動方程。這將是汽車在賽道水平路段的運動情況，此時忽略了摩擦力和車輪旋轉。在這種情況下，運動方程為

$a(t)=0\,;\,v(t)=v_{0}\,;\,d(t)=v_{0}t+d_{0}\,$,

其中，*a(t)* 為加速度，*v(t)* 為速度，*d(t)* 為時間為 *t* 時的距離。時間 *t=0* 時的初始距離和速度分別由 $d_{0}$ 和 $v_{0}$ 給出。

重力作用在墜落物體上的力

錘子和羽毛下降 - 阿波羅 15 號指令長大衛·斯科特證明伽利略是正確的。（1.38 MB，ogg/Theora 格式）。

首先考慮最基本情況，即質量為 *M* 的墜落物體（一個蘋果？）。重力作用於該物體上的力由以下表達式給出：

$F_{g}=Mg\,$,

其中 *g* 是 重力加速度 (9.807 米/秒² = 32.17 英尺/秒²，在地球表面)。該力向下作用，導致物體加速向地球墜落。

該物體的運動方程（忽略摩擦力）如下：

$a(t)=g\,;\,v(t)=gt+v_{0}\,;\,d(t)={\frac {1}{2}}gt^{2}+v_{0}t+d_{0}\,$.

一個物體從 4 英尺（1.22 米）的高度落下需要 0.499 秒才能到達地面，並且最終速度達到 4.892 米/秒。如果該物體隨後立即被轉向在沒有摩擦力的 24 英尺的平坦軌道上滑動，那麼它將需要額外的 1.496 秒才能滑完整個軌道，總共需要 1.995 秒。

重力對松木賽車的影響

松木賽車不會直接向下墜落，而是沿著傾斜角為 $\theta$ 的斜坡向下行駛。只有沿軌道表面方向的重力分量才會導致賽車的加速度。由此產生的加速力為

$F_{a}=Mg\,\sin \theta \,$.

賽車只在傾斜角為 $\theta$ 的斜坡上加速。在平坦軌道部分，其中 $\theta =0$，此加速力變為零。這可以看作是具有減小的重力 $g_{\theta }$ 的加速度。

$g_{\theta }=g\,\sin \theta \,$.

這種減小的重力可以用於上述運動方程來求解賽車。在松木賽車初始坡度上，$v_{0}=0$ 且 $d_{0}=0$，因此（忽略摩擦力和車輪旋轉）這些方程變為

$a(t)=g_{\theta }=g\,\sin \theta \,;\,v(t)=g_{\theta }t\,;\,d(t)={\cfrac {1}{2}}g_{\theta }t^{2}\,$.

沿著斜坡滾下的時間 $T_{r}$ 由下式給出

$d(T_{r})=L_{r}={\cfrac {1}{2}}g_{\theta }T_{r}^{2}\,$,

求解 $T_{r}$

$T_{r}={\sqrt {\cfrac {2L_{r}}{g_{\theta }}}}={\sqrt {\cfrac {2L_{r}}{g\sin \theta }}}\,}$.

斜坡底部最大速度為

$v(T_{r})=v_{max}=g_{\theta }T_{r}={\sqrt {2gL_{r}\sin \theta }}={\sqrt {2gH}}\,$.

對於理想斜坡，$T_{r}$ = 0.998 秒，$v_{max}$ = 4.892 米/秒。這個時間是上面自由落體情況的兩倍，但獲得的最大速度相同！

汽車在賽道平坦部分($\theta =0$)的運動方程，當$t>T_{r}$時，由以下給出

$a(t)=0\,;\,v(t)=v(T_{r})=v_{max}\,;\,d(t)=L_{r}+v_{max}(t-T_{r})\,;\,t>T_{r}\,$.

完成賽道平坦部分所需時間$T_{f}$ 為

$d(T_{r}+T_{f})=L_{r}+L_{f}=L_{r}+v_{max}T_{f}\,$.

求解$T_{f}$

$T_{f}={\cfrac {L_{f}}{v_{max}}}\,$.

完成這場比賽的理想汽車總時間為

$T=T_{r}+T_{f}={\cfrac {v_{max}}{g_{\theta }}}+{\cfrac {L_{f}}{v_{max}}}\,$.

平軌時間為 1.4953 秒，總時間為 2.4933 秒。由於達到了與自由落體情況相同的最大速度，因此（無摩擦）平軌時間相同。總時間包括沿著斜坡向下移動的額外半秒。

能量守恆

透過能量考慮可以獲得對松木賽車物理的一些關鍵理解。透過這種思考，我們可以考慮系統中可用的勢能以及車輪中的線性動能和旋轉動能。上面我們只考慮了汽車沿斜坡向下移動和橫穿賽道時的線性運動。事實上，車輪的旋轉需要能量，從而從系統中消耗了本應用來加速汽車的能量。為了解釋車輪的旋轉，我們將考慮系統的能量。

我們將從系統中的勢能開始，然後轉向簡單的線性情況，最後加上車輪的旋轉。

勢能

使松木賽車沿斜坡滾下的能量是勢能（符號 $U_{g}$）。在斜坡底部，這種能量轉化為動能（符號 $E_{k}\,$）。

勢能可以用以下公式計算

$U_{g}=mgh\,$.

其中 m 是汽車的質量，$g$ 是重力加速度（在地球表面為 9.807 m/s² = 32.17 ft/s²），h 是汽車在起點斜坡上的高度（約 4 英尺 = 1.22 米）。一個 5 盎司的松木賽車中儲存的勢能約為 1.7 kg m²/s²= 1.7 J。1.7 焦耳的能量相當於 1.7 瓦的功率作用於一秒鐘。

平動動能

動能可以用以下公式計算

$E_{k}={\frac {1}{2}}mv^{2}$.

其中 v 是汽車的速度（速度），以米每秒（國際單位制）測量。如果所有的勢能都轉化為動能，那麼

$U_{g}=E_{k}\,$

並且，從上面代入，

$mgh={\frac {1}{2}}mv^{2}\,$

由於質量在等式兩邊，您可以將兩邊都除以 $m$ 並取消（移除）等式中的質量。

$gh={\frac {1}{2}}v^{2}\,$

並且，重新排列，速度可以從以下公式中找到

$v={\sqrt {2gh}}\,$

速度不取決於質量，正如伽利略在比薩斜塔上所證明的那樣，在阿波羅 15 號著陸期間，大衛·斯科特在月球上進行了證明。任何從 1.219 米高處墜落物體的速度都是 4.890 m/s（11 英里/小時）。

旋轉動能

向前移動並不是唯一的動能；旋轉車輪也需要能量。每個車輪的旋轉動能由以下公式給出

$E_{r}={\frac {1}{2}}I\omega ^{2}$,

其中 I 是車輪的慣性矩，ω 是角速度。由於我們只考慮車輪在賽道上不打滑的情況，因此角速度與線速度的關係為

$\omega =v/r\,$,

其中r是輪子的半徑。一個半徑為 r 且質量為 $m'$ 的圓環的慣性矩為

$I_{ring}=m'r^{2}\,$

對於圓盤，它為

$I_{disk}={\frac {1}{2}}m'r^{2}\,$

對於一個松木賽車輪，慣性矩可以近似為

$I=0.58\,mr^{2}\,$,

其中m是一個輪子的質量，r是輪子的半徑。

因此，N個輪子的轉動動能為

$E_{r}={\frac {N}{2}}(0.58\,mr^{2})\omega ^{2}={\frac {N}{2}}(0.58\,m)v\,^{2}\,$.

事實證明，在汽車最高速度 4.75 米/秒時，四個輪子中儲存的能量為 0.094 焦耳（見下表）。與上面的 1.7 焦耳重力勢能相比，幾乎 6% 的能量儲存在旋轉的輪子中，大約 94% 的能量可用於汽車的向前速度。

如果我們再次將所有勢能轉化為動能，我們可以找到最大動能和速度

$U_{g}=E_{k}+E_{r}\,\Longrightarrow \,MgH={\frac {1}{2}}\left(Mv_{max}^{2}+0.58N\,mv_{max}\,^{2}\right)\,$.

求解速度，

$v_{max}={\sqrt {\cfrac {2gH}{1+0.58N{\cfrac {m}{M}}}}}\,={\sqrt {\cfrac {2gH}{\alpha _{R}}}}\,$

注意，這個結果再次獨立於賽道的幾何形狀。旋轉因子，它具有降低重力的效果，表示如下

$\alpha _{R}=1+0.58N{\cfrac {m}{M}}\,$.

此因子可與上述運動方程中的重力一起使用。它必須與由於賽道坡度引起的降低的重力相結合。所得的有效重力為

$g'_{\theta }={\cfrac {g\sin \theta }{\alpha _{R}}}\,$.

這個帶有輪子旋轉的降低的重力可以代入運動方程，以計算汽車在任何點的距離、速度和加速度。運動方程變為

$a(t)=g'_{\theta }={\cfrac {g\sin \theta }{\alpha _{R}}}\,;\,v(t)=g'_{\theta }t\,;\,d(t)={\cfrac {1}{2}}g'_{\theta }t^{2}\,$.

現在很清楚為什麼最重的汽車是最快的：對於大的 M，$\alpha _{R}$ 接近 1，速度與無摩擦塊的上述情況相同：4.9 米/秒。使用標準 3.6 克車輪，一輛 141.7 克（5 盎司）的汽車在軌道底部具有 4.75 米/秒的速度。一輛 113.4 克（4 盎司）的汽車具有 4.72 米/秒的速度。

輕車輪的優勢也很明顯。速度最慢的汽車是車輪質量最大的汽車。如果$m=M$（四個 35 克車輪在軌道上滾動！）速度為 2.7 米/秒。使用 3.6 克車輪，速度為 4.75 米/秒；使用 1 克輕車輪，速度為 4.85 米/秒。另一種看法是，輕車輪汽車的動能在車輪中的比例小於 2%，而標準車輪汽車的動能在車輪中的比例接近 6%。

只要車輪不接觸地面，抬起一個車輪就會降低旋轉能量。三輪（3.6 克）汽車的速度為 4.78 米/秒，而抬高輕車輪的汽車可以達到 4.86 米/秒。

理想化軌道

現在我們知道了理想化汽車能跑多快，讓我們讓它在理想化軌道上跑起來。典型的松木賽車軌道長 32 英尺，其中 4 英尺用於起跑門和制動裝置，剩下 8.534 米用於行駛。軌道的第一個部分的坡度約為 20 度，有一個彎曲的過渡段，接著是一個平坦的段到終點。軌道可以用一個長度為$d_{1}$ 的直斜坡部分來近似，接著是一個長度為$d_{2}$ 的平坦部分。與使用彎曲軌道和數值積分 獲得的結果相比，使用直線軌道近似計算的時間差異小於 0.001 秒。 對於直線軌道和 20 度坡度，$d_{1}$ = 3.564 米，$d_{2}$ = 4.970 米。汽車從零速度開始沿著斜坡段$d_{1}$ 行駛，並加速到速度$v\,$，平均速度為$v/2\,$。然後它以速度$v\,$ 行駛距離$d_{2}$。總時間為

$t=2{\frac {d_{1}}{v}}+{\frac {d_{2}}{v}}$

或 12.098/v 秒，如果速度以米/秒為單位給出。下表給出了不同條件下的行駛時間。

汽車速度和時間

條件	$h\,(m)$	$m\,(g)$	$m'\,(g)$	$v\,(m/s)$	$t\,(s)$
無摩擦塊	1.219	任何	0	4.89	2.47
庫存車輪	1.219	141.7	3.6	4.75	2.55
輕型（4 盎司）汽車	1.219	113.4	3.6	4.72	2.56
輕型車輪	1.219	141.7	1.0	4.85	2.49
一個抬高的車輪	1.219	141.7	2.7	4.78	2.53
輕型車輪，一個抬高	1.219	141.7	0.75	4.86	2.49
後輪偏置（原裝車輪）	1.243	141.7	3.6	4.80	2.52

質心

到目前為止，我們已經將汽車近似為一個點質量，它從距離終點 1.219 米的高度開始，最終達到 0 米的高度。正如任何熟悉松木賽車的人都知道的那樣，通常最好將質心儘可能地向後移動，部分原因是為了增加重力勢能。將質心移到後面，汽車會快多少？考慮兩輛汽車，汽車 A 的質心位於木塊的中心，汽車 B 的質心位於擴充套件軸距配置的後面軸前 25.4 毫米（1 英寸），該軸距距離木塊後部 15.9 毫米（5/8 英寸）。汽車 B 的質心比汽車 A 後移 47.6 毫米，在 30° 斜坡上高出 23.8 毫米。汽車 A 從 1.219 米的高度開始，（如上所示）最大速度為 4.75 米/秒，時間為 2.55 秒；汽車 B 從 1.243 米的高度開始，最大速度為 4.80 米/秒，時間為 2.52 秒。

摩擦力

圖示說明作用在靜止在斜面上的木塊上的力。

摩擦 是兩個相互接觸的物體之間阻礙其相對運動的力。一般來說，摩擦力有兩種型別——靜摩擦和動摩擦。靜摩擦力是抵抗運動的力。動摩擦力也稱為滑動摩擦力，是在兩個相對運動的物體之間產生的力。與松木賽車相關的主要摩擦型別是車軸在車輪上的動摩擦和車輪在賽道上滾動時的靜摩擦。這兩個方面將在下面進一步詳細討論。空氣阻力被認為是一個特殊主題，將在下面詳細討論。

其他型別的摩擦，包括車輪內輪轂與車身、車輪外輪轂與車軸頭、車輪與賽道導軌之間的接觸，可以透過適當的汽車設計和調校來最大限度地減少或完全消除。

滑動（軸）摩擦

只要兩個表面相互接觸並處於相對運動狀態，就會發生滑動摩擦。對於松木賽車，接觸摩擦的主要來源是車軸在車輪上。這種摩擦發生在汽車“系統”內部，並且始終發生在金屬車軸與塑膠車輪之間。作用在車軸和車輪上的摩擦力 ($F'_{f}$) 如下

$F'_{f}=\mu N_{f}\,$,

其中 $N_{f}$ 是表面之間產生的正壓力（垂直於接觸面），$\mu$ 是摩擦係數。摩擦係數是兩個相互接觸的材料的屬性。對於松木賽車，$\mu$ 的值為光滑塑膠對金屬約為 0.24，如果車軸經過拋光並使用石墨等潤滑劑，可以降低到 0.10 或更低。

正壓力是車身質量對車軸的力。在斜坡為 $\theta$ 的賽道上，所有承載車軸的總正壓力為

$N_{f}=(M-Nm)g\cos \theta \,$,

其中 M 是汽車的質量，m 是車輪的質量，N 是承載車輪的數量。$M-Nm$ 對於一輛最大重量的汽車來說是 127.3 克，它有四個 3.6 克的承載車輪。

相對於賽道的摩擦力會因機械優勢而降低，機械優勢是車輪半徑與車輪軸孔半徑的比率。車輪每旋轉一次，汽車行駛一個車輪周長：95.0 毫米。車軸每次旋轉只在車輪軸孔周長上行駛 7.19 毫米。然後，車輪對車軸的摩擦力為

$F_{f}=\mu \left({\cfrac {r}{r_{B}}}\right)(M-Nm)g\cos \theta =\mu '(M-Nm)g\,$,

其中 $r_{B}$ 是車輪軸孔的半徑，調整後的摩擦係數 $\mu '$ 為

$\mu '=\mu \left({\frac {r}{r_{B}}}\right)\,$.

由該力引起的線性加速度，包括車輪旋轉的影響，與運動方向相反，並且為

$a'_{f}={\cfrac {\mu 'g\left(1-{\cfrac {Nm}{M}}\right)\cos \theta }{\alpha _{R}}}={\cfrac {\mu 'g\alpha _{m}\cos \theta }{\alpha _{R}}}\,}$,

其中車輪質量因子 $\alpha _{w}$ 已被定義為

$\alpha _{w}=1-{\frac {Nm}{M}}\,$.

由於這是一個恆定加速度，它可以在運動方程中寫成一個有效減少的重力。到目前為止，所有幾何、旋轉和滑動摩擦效應的減少重力為

$g'_{\theta f}=g{\cfrac {\sin \theta -\mu '\alpha _{w}\cos \theta }{\alpha _{R}}}\,$.

使用以上值，車輪到軸承的摩擦力為 0.00946 牛頓。

請注意，由於車身質量更大（137.7 克車身加上四個 1.0 克車輪），輕輪車的車輪到軸承的摩擦力比標準輪車的摩擦力大 8%。但是，使用針式軸承可以將摩擦力減少一半，一些公開級別的比賽允許使用針式軸承。1 毫米針式軸承的機械優勢為 30，摩擦力為 0.00453 牛頓（假設為輕輪）。

另一個結果是，抬起的車輪不會減少車輪到軸承的摩擦力。三輪車只是將重量分配到三個軸承上而不是四個軸承上，摩擦力是相同的。所有抬起的車輪優勢都來自於旋轉動能。

滾動摩擦

摩擦有兩種：靜摩擦和動摩擦。靜摩擦是靜止物體所受到的阻力，例如，靜止在混凝土地板上的重箱子。滾動阻力 是滾動車輪與表面之間的摩擦。它是一種靜摩擦，因為即使車輪在移動，它也沒有與表面滑動。動摩擦是阻礙運動物體運動的力。使用箱子為例，當您在地板上滑動箱子時，必須克服的就是這種力。在車輪的例子中，滾動阻力是靜止的，而滑行 或燒胎 涉及動摩擦。從這個意義上說，滾動阻力在很大程度上對松木賽車來說是一種“良好”的摩擦，因為它所做的功很少，並且因為它有助於將本來會是滑行摩擦的摩擦轉化為車輪和軸承之間明顯更小的摩擦。

滾動阻力產生的力由下式給出

$F_{r}=C_{rr}N\,$

其中 C_rr 是滾動摩擦係數 (CRF)，而$N$ 是法向力（垂直於軌道）。低滾動阻力輪胎的 CRF 值約為 0.002（參見滾動阻力 文章）。

在斜率為 $\theta$ 的軌道上，法向力垂直於軌道，由下式給出

$N_{\theta }=Mg\cos \theta \,$.

然後來自滾動阻力的摩擦力為

$F_{\theta r}=C_{rr}Mg\cos \theta \,$.

該力作用在與汽車運動方向相反的方向上。由該力引起的線性加速度為

$a'_{\theta rr}=g'C_{rr}\cos \theta ={\cfrac {gC_{rr}\cos \theta }{\alpha _{R}}}\,}$,

導致有效滾動阻力降低的重力為

$g'_{\theta rr}=g{\cfrac {\sin \theta -C_{rr}\cos \theta }{\alpha _{R}}}\,$,

滾動阻力降低的重力可以代入運動方程，以求解汽車在任何時間點的距離、速度和加速度。

在平坦的路段上，$\theta =0$ 並且

$F_{r}=C_{rr}Mg=0.002\times 0.1417\,kg\times 9.807\,m/s^{2}=0.0028\,N\$.

輪軸摩擦和滾動阻力的大小相當。從上面一節，滾動阻力估計約為0.003 N，而上面估計的輪軸摩擦大約是它的三倍。

可以降低CRF的汽車改裝可以將滾動阻力降低相同的倍數。例如，“V”或“H”胎面花紋限制了車輪與軌道之間的接觸面積，從而降低了CRF和滾動阻力。需要注意的是，抬高的車輪不會降低整體滾動阻力，因為汽車的全部重量分佈在剩餘的三個車輪上，並增加了它們的滾動阻力。然而，後輪驅動的汽車的後輪的滾動阻力更大，因為它們承受了更大的重量比例。

帶摩擦的運動

包括軌道幾何形狀、車輪旋轉、滑動摩擦和滾動摩擦的影響的“全部”降低的重力為

$g'_{\theta fr}={\cfrac {g_{\theta fr}}{\alpha _{R}}}=g{\cfrac {\sin \theta -\mu '\alpha _{w}\cos \theta -C_{rr}\cos \theta }{\alpha _{R}}}\,$.

注意，降低的重力可能是負數。特別是，當 $\theta =0$ 時，它在平坦的軌道上是負數。另一個有趣的現象是，$\theta$ 將存在一個最小值，低於該值，汽車將永遠無法克服摩擦力並開始滾動——即使在傾斜的軌道上！

運動方程變為

$a(t)=g'_{\theta fr}\,;\,v(t)=g'_{\theta fr}t+v_{0}\,;\,d(t)={\cfrac {1}{2}}g'_{\theta fr}t^{2}+v_{0}t+d_{0}\,$.

比賽開始時，$v_{0}=0$ 和 $d_{0}=0$。當到達平坦路段的起點時，只需將時間重置為零，並使用 $\theta =0$，$v_{0}=v_{max}$（您必須根據這些方程式計算 $v_{max}$） 和 $d_{0}=L_{r}$。

測量摩擦力

可以使用圖 1 中的裝置測量靜摩擦力和動摩擦力。^[3] 從 牛頓第二運動定律，我們知道力是平衡的，因此法向力平衡了汽車上的重力。

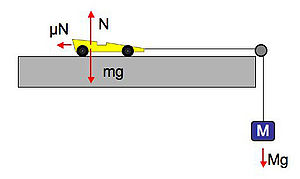圖 1. 測量平坦表面上的摩擦係數。

$N_{f}=mg\,$.

當質量 M 恰好平衡靜摩擦力時

$\mu N_{f}=mg\,$

以及

$\mu =M/m\,$ .

圖 2. 測量傾斜表面上的摩擦係數。

讀者可以驗證，在圖 2 所示的傾斜情況下，摩擦係數由以下公式給出

$\mu ={\frac {\left({\frac {M}{m}}-\sin(\theta )\right)}{\cos(\theta )}}\,$.

可以使用上述任何一種裝置來確定動摩擦力，但操作過程需要更多耐心。增加或減少質量 M，直到在推動汽車時，汽車以恆定速度運動。此時，重力等於動摩擦力。訣竅是汽車不能加速也不能減速；我們希望 F=ma=0，但這次汽車是在運動中。

空氣阻力

氣體或液體對物體的摩擦力稱為 阻力，阻力 F_d 可以透過以下公式計算。^[4]

$\mathbf {F} _{d}={1 \over 2}\rho AC_{d}v^{2}=bv^{2}$

其中 ρ 是空氣密度（約為 1.2 kg/m³），v 是空氣相對於物體的速度，A 是物體的正面面積，C_d 是 阻力系數，它取決於車輛的形狀和表面（但對於典型的汽車，大約為 0.4）。常數 b 在上面定義為一個約定。對於一輛松木賽車，A 取決於汽車的設計——未切割的木塊為 0.0014 m²。對於一輛使用標準車輪的 5 盎司的汽車，其速度為 4.75 m/s，產生的阻力為 0.0081 N。使用 $F=ma$，我們得到加速度為 -0.057 kgm/$s^{2}$，約為重力的 0.6%，但這仍然足以使汽車在賽道平坦路段的減速從 4.75 m/s 降至 4.69 m/s。^[5] 類似賽道的數值積分表明，比賽時間慢了 1.8%。^[6] 實際上，所有汽車都會受到一定的空氣阻力，但低矮流暢的設計可能比空氣動力學較差的汽車快幾百分之一秒。

在松木賽車的尺寸和速度下，空氣的 粘度完全無關緊要；唯一重要的空氣阻力是阻力，它與空氣密度和速度的平方成正比。阻力是一種 衝擊壓力。

要得到受衝擊壓力阻力影響的車輛的運動方程，我們考慮一輛在傾斜軌道上行駛的汽車，其車輪旋轉並受到摩擦力，並在此模型中加入空氣阻力。根據力的平衡，汽車的加速度為以下公式

${\frac {\mathbf {F} _{d}}{M}}=a(t)={\cfrac {g_{\theta fr}-{\frac {b}{M}}v^{2}}{\alpha _{R}}}$,

回顧一下，力與加速度透過牛頓第二運動定律有關，加速度是速度的導數。因此，運動速度方程可以寫成

這是一個關於速度的非線性微分方程。它的解並不直接，但可以求解。運動方程為

$a(t)=g'_{\theta fr}\left[1-\tanh ^{2}\left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\right]\,$,

$v(t)={\sqrt {\frac {g'_{\theta fr}\alpha _{R}M}{b}}}\tanh \left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\,$,

$d(t)={\frac {\alpha _{R}M}{b}}\ln \left[\cosh \left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\right]\,$.

摩擦學

石墨的分子結構。碳原子是形成六邊形平面結構的灰色球體。這些平面可以很容易地相互滑動，使塊狀石墨變得光滑。

摩擦學是研究摩擦、潤滑和磨損的學科。由於摩擦是減緩松木賽車速度的力，而潤滑可以減少摩擦，因此摩擦學是這項運動中必不可少的科學。磨損不是一個重要的考慮因素，因為正如我們在上面看到的那樣，力很小。潤滑劑必須減少車輪和軸之間的摩擦，並且必須與聚苯乙烯車輪相容。膨脹的聚苯乙烯被稱為泡沫塑膠，是熱可可的絕佳杯子，但卻是裝有機溶劑（如汽油或萘，問問你爸爸關於舊汽車修理店的技巧）的糟糕容器。純聚苯乙烯可以交聯，與聚丁二烯形成共聚物，被稱為高抗衝聚苯乙烯 (HIPS) 或高抗衝塑膠。HIPS 非常適合注塑成型，因此松木賽車車輪使用它並不偶然。儘管如此，仍應注意防止不合適的溶劑，潤滑劑、油漆或清潔劑遠離車輪。潤滑的另一個考慮因素是可能會用過量的潤滑劑（尤其是液體）弄髒賽道。出於這個原因，一些比賽規則只允許使用乾粉潤滑劑。

二硫化鉬 (MoS₂) 的 X 射線晶體結構。鉬是藍色，硫是黃色。

石墨

石墨，與鑽石一樣，是碳的幾種形式之一。與鑽石不同，石墨是一種劣質寶石，但它是一種極好的潤滑劑。這是因為鑽石中的化學鍵形成三維結構，而石墨中的化學鍵形成二維結構。石墨的二維片材可以輕鬆地相互滑動，使石墨粉末具有潤滑特性。

二硫化鉬

二硫化鉬的化學式為 MoS₂，其化學結構與石墨類似，因為它形成了相互滑動的二維層。在松木賽車的應用中，二硫化鉬粉末通常與石墨粉末混合。

特氟龍

特氟龍是杜邦公司對聚四氟乙烯 (PTFE) 的品牌名稱，它是一種合成的氟聚合物（一種含有氟的聚合物）。特氟龍具有所有已知固體材料中最低的摩擦係數。它以粉末形式用作松木賽車潤滑劑。