A-level 物理/宇宙學/已知宇宙模型

隨著更先進的工具的開發，我們對宇宙的理解也得到了改善。一些提出的宇宙模型被證明是錯誤的，而其他想法至今仍存在。

測量宇宙中的距離

宇宙尺度的距離是巨大的，我們日常使用的米甚至公里都太小了。我們需要使用更適合大距離的單位。通常，其他單位使用起來很方便，因為它們是透過測量得到的。

光年

一光年定義為光在一年內傳播的距離。如你所知，光速為 $3\times 10^{8}$ ${\text{ms}}^{-1}$，因此它在一年的時間內傳播的距離非常巨大。一光年大約為 $10^{16}{\text{m}}$.

天文單位

天文單位定義為地球和太陽之間的平均距離。它起源於這樣一個事實：可以測量行星的距離，但只能以地球和太陽之間的距離為倍數。它在今天仍然適用於太陽系內的距離。它大約等於 $1.5\times 10^{11}{\text{m}}$.

視差的簡化示例。

秒差距

一秒差距僅僅是恆星從地球軌道上的兩個對立點觀察時視差角的一半的倒數。視差是指當觀察者位置改變時，物體相對於固定背景的視位置的變化，就像你在汽車裡時，建築物看起來比背景山丘移動得更快一樣。它從測量的角度方便地求出，因此主要用於恆星的距離。這個概念將在 恆星和星系 中詳細介紹。一秒差距大約為 $3\times 10^{16}{\text{m}}$，或者 3.26 光年。

太陽系的概述

太陽系，顯示了太陽、行星、火星和木星之間的小行星帶，以及一顆彗星。

我們的太陽系包括太陽、行星和一個小行星帶。此外，還有彗星，它們具有高度橢圓的軌道，並定期返回太陽系。

行星

有八顆行星繞太陽執行（冥王星被重新歸類為矮行星），太陽位於太陽系的中心。大多數行星也有天然衛星，或稱為衛星，繞它們執行。下表概述了行星相對於地球的主要特徵。

行星	赤道 直徑	質量	軌道 半徑 (天文單位)	軌道週期 (年)	軌道 傾斜 角度 (°)	軌道 偏心率	日 (天)	衛星
水星	0.382	0.06	0.387	0.241	7.00	0.206	58.6	無
金星	0.949	0.82	0.72	0.615	3.39	0.0068	-243	無
地球	1.00	1.00	1.00	1.00	0.00	0.0167	1.00	1
火星	0.53	0.11	1.52	1.88	1.85	0.0934	1.03	2
木星	11.2	318	5.20	11.86	1.31	0.0484	0.414	63
土星	9.41	95	9.54	29.46	2.48	0.0542	0.426	49
天王星	3.98	14.6	19.22	84.01	0.77	0.0472	-0.718	27
海王星	3.81	17.2	30.06	164.8	1.77	0.0086	0.671	13
冥王星	0.18	0.002	39.5	248.5	17.1	0.249	-6.4	4

小行星帶

火星和木星之間存在著小行星的密集區域，被稱為小行星帶。有成千上萬顆這樣的類行星繞太陽執行，有時也被稱為小行星。

彗星

彗星是由岩石、冰凍水、甲烷和氨組成的團塊，繞太陽執行，通常只有幾公里寬。它們擁有非常偏心（橢圓形）的軌道，因此它們與太陽之間的距離變化很大。當它們靠近太陽時，由於太陽輻射，它們會有長達 1 個天文單位的尾巴。

對宇宙的理解進步

太陽系的公認模型在過去幾十年中一直備受爭議。在舊的地心說模型中，地球最初被置於太陽系的中心，其他行星和太陽圍繞它執行。現在，公認的模型將太陽置於中心，地球和其他行星圍繞它執行。

哥白尼

火星的逆行運動

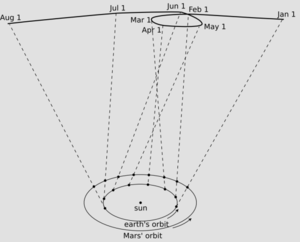
尼古拉·哥白尼發現舊的地心說模型過於複雜。他決定將太陽而不是地球置於宇宙的中心，這就是我們現在所說的日心說模型。這個模型可以很容易地解釋行星和太陽在天空中運動的情況，尤其是火星的逆行運動，即火星在天空中的運動方向似乎會在幾周內“倒退”。以前人們用本輪來解釋這種火星的逆行運動，認為它會在某些點進行“迴圈運動”。哥白尼的新模型解釋說，由於地球比火星離太陽更近，在地球“超越”火星的階段，火星在天空中的運動方向看起來會“倒退”。

對哥白尼的反對

哥白尼的日心說模型主要因為當時人們的宗教信仰而遭到大多數人的拒絕，儘管它似乎簡化了行星的運動，但它在擬合觀測到的行星運動方面不如地心說準確。

人們還認為，如果地球在運動，恆星應該會有可檢測的視差。哥白尼聲稱恆星距離太遠，無法檢測到任何視差，隨著更靈敏裝置的出現，他現在被證明是正確的。另一個反對日心說的論點是，所有物體都朝地球落下，因此地球一定是宇宙的中心。這在牛頓徹底改變我們對運動的認識之前是人們直觀的結論。

開普勒

以太陽為一個焦點的橢圓軌道

約翰內斯·開普勒透過使用橢圓軌道而不是圓形軌道來改進哥白尼的原始模型。他制定了行星運動的三大定律。

開普勒第一定律

開普勒發現，如果行星在橢圓而不是圓形軌道上運動，並且太陽位於這些橢圓的其中一個焦點上，那麼行星更符合觀測到的模式。因此，開普勒第一定律指出

行星以太陽為一個焦點的橢圓軌道繞太陽執行。

開普勒第二定律

等時間內掃過等面積

現在行星有了橢圓軌道，它們在軌道上的所有點以相同速度運動就沒有意義了。行星在靠近太陽時會加速，在遠離太陽時會減速。開普勒觀察到，如果行星軌道的兩個點之間的時差相同，則由行星在兩個點上的位置和太陽形成的虛線三角形始終具有相同的面積。由此得出，行星在靠近太陽時比遠離太陽時執行得更快。開普勒第二定律指出

連線行星和太陽的直線在等時間內掃過等面積。

橢圓的長半軸

開普勒第三定律

開普勒意識到，行星到太陽的距離與其軌道週期之間存在關係：$T^{2}\propto d^{3}$，其中 T 是繞太陽執行一週所需的時間，d 是到太陽的距離，但實際上是長半軸的長度（即橢圓最長直徑的一半）。

軌道週期的平方與到太陽距離的立方成正比。

伽利略

金星的相位。

伽利略·伽利雷是第一個使用望遠鏡觀測夜空的人。他能看到肉眼看不到的許多東西，比如月球表面不完美，以及天空中有許多暗淡的星星。這兩點都支援了哥白尼的觀點。

伽利略和金星

當伽利略用他的望遠鏡觀察金星時，他注意到金星像月球一樣經歷相位變化。他還注意到，當金星呈新月狀時，它比滿月時要大得多。這一觀察結果證明了金星繞太陽而不是地球執行。

伽利略和木星的衛星

伽利略還觀察到四個天體繞木星執行，這些天體現在被稱為伽利略衛星。它們支援了並非所有天體都繞地球執行的觀點。

牛頓的萬有引力定律

當艾薩克·牛頓建立他的萬有引力定律時，他試圖證明開普勒對行星運動的觀察與他的定律一致。這有力地證明了他是正確的。

牛頓的萬有引力定律可以用來給出行星的公式形式$T^{2}\propto d^{3}$

太陽與行星之間的萬有引力等於使行星保持在軌道上所需的向心力。

$F=G{\frac {m_{1}m_{2}}{d^{2}}}={\frac {mv^{2}}{d}}$

行星軌道週期的計算公式為

${\text{Time taken}}={\frac {\text{distance}}{\text{velocity}}}$

其中，距離為圓周長，即 $2\pi \times d$ （注意，d 為距離太陽的距離，即半徑，不是直徑）。 因此，我們有

$T={\frac {2\pi d}{v}}$

我們可以將公式重新整理，使 v 成為主體，並將它代入到向心力公式中的 $v^{2}$

$v={\frac {2\pi d}{T}}$

$v^{2}={\frac {4\pi ^{2}d^{2}}{T^{2}}}$

$G{\frac {m_{1}m_{2}}{d^{2}}}={\frac {4\pi ^{2}md}{T^{2}}}$

消除行星質量 m，並將公式整理

$G{\frac {mT^{2}}{4\pi ^{2}d^{3}}}=1$

最後，將 $T^{2}$ 作為主體

$T^{2}={\frac {4\pi ^{2}}{Gm}}d^{3}$

我們現在得到了一個 $T^{2}\propto d^{3}$ 的形式，比例常數為 ${\frac {4\pi ^{2}}{Gm}}$，其中 m 為太陽的質量。

海王星的發現

1821 年，亞歷克西斯·布瓦爾德發表了關於天王星軌道非常準確的觀測結果。但是，不久之後，天王星的軌道被發現偏離了發表的數值。 1845 年，約翰·亞當斯利用牛頓的萬有引力定律計算了天王星軌道外另一顆行星的軌道，該行星的引力可以解釋天王星軌道上的 **擾動**。 海王星在一年後被發現於其預測的位置。 冥王星的發現也是透過類似的方法，因為它導致了天王星和海王星軌道上的進一步擾動。

牛頓理論遇到的問題

儘管牛頓的理論在解釋行星運動方面非常成功，甚至被用來發現未知行星，但它仍然存在一些問題。

• 觀測發現水星的軌道與該理論預測的軌道不同。現在，愛因斯坦的廣義相對論已經解決了這個問題。
• 如果宇宙中每個物體都相互吸引，那麼整個宇宙就應該由於引力吸引而坍縮。為了解決這個問題，牛頓提出了一個想法，即宇宙是無限大的，物質均勻地分佈在整個宇宙中。然而，這導致了它自己的問題，即奧伯斯佯謬，該佯謬指出，一個無限大的宇宙在任何給定的視線方向上始終會有一個恆星，因此夜空實際上應該很亮。這個矛盾已經被埃德溫·哈勃觀測到的宇宙膨脹解決了。