A-level 物理/力學、場與能量/萬有引力場

我們已經接觸過萬有引力場，其中行星的萬有引力場強乘以物體的質量就等於該物體的重量，地球的萬有引力場強 $g$ 等於其表面上的自由落體加速度 $9.81\,\mathrm {ms^{-2}}$。現在我們將考慮不均勻的萬有引力場，以及如何計算 $g$ 的值，針對任何給定的質量。

萬有引力場

地球的萬有引力作用範圍延伸到太空中很遠的地方。例如，月球受到地球萬有引力的影響，即使它距離地球 400,000 公里（在那裡萬有引力是向心力）。地球有一個萬有引力場，會吸引任何有質量的物體朝向地球中心。

徑向場

地球的徑向萬有引力場由這些線表示。

萬有引力場是包圍地球的一個區域，在這個區域中，另一個物體會感覺到引力。該力的方向朝向地球中心，或者一般來說是朝向質量中心。距離越遠的物體感受到的引力越小，而距離越近的物體感受到的引力越大。

均勻場

萬有引力場線表示是任意的，如這裡所示，在 30x30 網格到 0x0 網格中表示，幾乎平行且直指地球中心。

地球的萬有引力場由小尺度上的平行線表示。

然而，**均勻場**的線完全平行。地球的萬有引力場可以認為在汽車、球和飛機等小物體尺度上是均勻的。在這個尺度上，對於較小的高度（幾十公里），場強的變化不足以察覺。同樣，箭頭指向地球中心，因為物體就是那樣下落的。

牛頓的萬有引力理論

艾薩克·牛頓試圖找到一種方法來解釋為什麼物體落向地球中心而不是僅僅停留在原地。他開始將蘋果下落與月球“落向”地球聯絡起來，並提出了他的**萬有引力定律**。

他認為，任何兩個有質量的物體之間都會存在引力。這種引力與它們的質量成正比，因此質量越大的物體之間的引力就越強。

每個物體的萬有引力場都是徑向場，因為質量集中在物體的中心，如你所知，這就是萬有引力可以被認為起作用的地方。

如你所見，當距離加倍時，四分之一的力線穿過該平面。

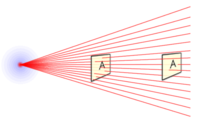
徑向場的強度隨著你離它越遠而減弱。正如你在右邊圖中看到的，穿過該平面的場線數量在距離加倍時變為四分之一，如果距離增加三倍，它將是原始值的 ${\frac {1}{9}}$。

這被稱為平方反比定律，對於任何點源來說都是成立的，比如來自一個點的光或輻射量。

平方反比定律遵循 ${\frac {1}{r^{2}}}$。

利用以上，牛頓認為引力與兩個質量以及它們之間的距離成正比

$F\propto {\frac {m_{1}m_{2}}{r^{2}}}$.

這種關係是牛頓萬有引力定律通常表述的基礎

任何兩個點質量都相互吸引，吸引力與它們的質量成正比，與它們之間距離的平方成反比。

然而，要將其轉化為一個方程，我們需要新增一個比例常數 G

$F=-G{\frac {m_{1}m_{2}}{r^{2}}}$.

其中 G 是**萬有引力常數**，$6.67\times 10^{-11}\ \mathrm {N\cdot m^{2}\cdot kg^{-2}}$。方程中還有一個負號，這將在“電場”模組中解釋，在那裡我們將遇到排斥力和吸引力。

$F=-G{\frac {m_{1}m_{2}}{r^{2}}}$ 也有時寫成 $F=-G{\frac {Mm}{r^{2}}}$，這樣大寫的 M 就代表行星這樣的巨大質量，而小寫的 m 就代表球或飛機這樣的較小質量。

萬有引力場強

定義萬有引力場強

萬有引力場強告訴我們萬有引力場有多強。你可能還記得，地球表面附近的萬有引力場強為 $9.81\,\mathrm {m/s^{2}}$。這意味著在地球表面附近的物體將以 $9.81\,\mathrm {m/s^{2}}$ 的加速度朝它加速。然後我們可以將萬有引力場強定義為物體在該萬有引力場中將經歷的加速度。

然而，一個更好的定義可以從方程 $F=ma$ 推匯出。使 $a$ 成為該方程的主體，我們得到 $a={\frac {F}{m}}$，或 $g={\frac {F}{m}}$。從這個方程的排列方式，我們對萬有引力場強的定義現在變成了

某點處的萬有引力場強是在該點放置的單位質量所受到的萬有引力。

這意味著萬有引力場強 $g$ 等於 1 kg 質量在該萬有引力場中所受到的力。

從新的定義來看，萬有引力場強是用 $\mathrm {N\ kg^{-1}}$ 測量的，雖然在將其視為加速度（如自由落體中的物體的加速度）的情況下，使用 $\mathrm {ms^{-2}}$ 是完全可以接受的。

求質量的場強

由於 $F=-G{\frac {Mm}{r^{2}}}$ 以及 $\ F=mg$，它們可以組合得到

$mg=-G{\frac {Mm}{r^{2}}}$ （將 F 替換為 mg）

$g=-G{\frac {M}{r^{2}}}$ （透過約去小寫 'm'）

您可以使用此公式來求解特定點 r 處質量的重力場強度。

請注意，地球表面附近的重力場強度在數值上等於自由落體的加速度，$9.81\ \mathrm {ms^{-2}}$。