感覺系統/計算機模型/神經模擬

感覺系統

視覺
聽覺
平衡
觸覺
嗅覺
味覺

技術方面

植入物
模型

動物中的感覺系統

鳥類
魚類
海洋動物
節肢動物
其他動物

模擬動作電位

動作電位

“動作電位”是在神經系統中傳播訊號所使用的典型電壓變化。

動作電位 – 時間依賴性

使用下面描述的機制，傳入刺激（任何型別的刺激）都可能導致神經細胞的電壓電位發生變化。在達到某個閾值之前，這就是全部內容（圖 4 中的“失敗啟動”）。但是，當電壓門控離子通道的閾值達到時，就會發生反饋反應，幾乎立即完全開啟Na+離子通道（下面的“去極化”）：這使得Na+的通透性（在靜息狀態下約為K+通透性的1%）比K+的通透性大20倍。總的來說，電壓從大約-60mV上升到大約+50mV。在這一點上，內部反應開始關閉（並阻斷）Na+通道，並開啟K+通道以恢復平衡狀態。在此“不應期”期間（約1毫秒），任何去極化都不能引發動作電位。只有當靜息狀態恢復時，才能觸發新的動作電位。

要模擬動作電位，我們首先必須定義細胞膜的不同組成部分，以及如何用分析方法描述它們。

細胞膜

細胞膜由一層拒水的、幾乎不可滲透的蛋白質雙層組成，即細胞膜。訊號處理的真正能力並非來自細胞膜，而是來自嵌入該膜中的離子通道。離子通道是嵌入細胞膜中的蛋白質，可以選擇性地為某些型別的離子開啟。（這種選擇性是由構成離子通道的氨基酸的幾何排列實現的。）除了上面提到的Na+和K+離子外，神經系統中通常存在的離子還有陽離子Ca2+、Mg2+和陰離子Cl-。

離子通道的狀態

離子通道可以處於三種狀態之一

• 開放（例如，開放的Na通道允許Na+離子透過，但阻止所有其他型別的離子）。
• 關閉，但可以開啟。
• 關閉，且無法開啟。

靜息狀態

典型預設情況——當沒有任何事情發生時——的特點是K+通道是開啟的，而其他通道是關閉的。在這種情況下，兩種力決定了細胞電壓

• K+細胞內和細胞外濃度之間的（化學）濃度差，這是由上述離子泵的持續活動產生的。
• 細胞內外之間的（電）電壓差。

平衡由能斯特方程定義

${{E}_{X}}={\frac {RT}{zF}}\ln {\frac {{[X]}_{o}}{{[X]}_{i}}}$

R ... 氣體常數，T ... 溫度，z ... 離子化合價，F ... 法拉第常數，[X]_o/i … 離子在細胞外/內的濃度。在 25°C 時，RT/F 為 25 mV，這導致靜息電位為

${{E}_{X}}={\frac {25mV}{z}}\log {\frac {{[X]}_{o}}{{[X]}_{i}}}$

對於神經元內部和外部典型的 K+ 濃度，這將產生 $E_{K+}=-75mV$。如果同時考慮 K+、Na+ 和 Cl- 的離子通道，則平衡狀態由戈德曼方程描述

${{V}_{m}}={\frac {RT}{F}}\ln {\frac {{{P}_{K}}{{[{{K}^{+}}]}_{o}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{o}}+{{P}_{Cl}}{{[Cl-]}_{i}}}{{{P}_{K}}{{[{{K}^{+}}]}_{i}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{i}}+{{P}_{Cl}}{{[Cl-]}_{o}}}}$

其中 Pi 表示離子“i”的通透性，I 表示濃度。使用典型的離子濃度，細胞在其靜息狀態下具有約 -60 mV 的負極性。

離子通道的啟用

離子通道的一個顯著特徵是它們的通透性可以透過以下方式改變：

• 機械刺激（機械啟用離子通道）
• 化學刺激（配體門控離子通道）
• 或外部電壓（電壓門控離子通道）
• 有時離子通道直接連線兩個細胞，在這種情況下，它們被稱為間隙連線通道。

重要

• 感覺系統基本上是基於離子通道的，這些離子通道被機械刺激（壓力、聲音、運動）、化學刺激（味覺、嗅覺）或電磁刺激（光）啟用，併產生“神經訊號”，即神經細胞中的電壓變化。
• 動作電位利用電壓門控離子通道快速可靠地改變神經元的“狀態”。
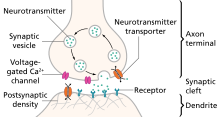
• 神經細胞之間的通訊主要利用由神經遞質啟用的離子通道，即前一個神經元在突觸處釋放的化學物質。這為神經訊號的處理提供了最大的靈活性。

電壓依賴性離子通道的建模

歐姆定律將電阻器的電阻 R 與其透過的電流 I 和電阻器兩端的電壓降 V 聯絡起來

$V=IR$

或

$I=gV$

其中 $g=1/R$ 是電阻的電導。如果現在假設電導與通道處於開放構象的機率成正比，則該方程變為

$I={{g}_{\max }}*n*V$

其中${g}_{max}$是通道的最大電導，而$n$是通道處於開放構象的機率。

示例：鉀離子通道

電壓門控鉀離子通道 (Kv) 只能處於開放或關閉狀態。設 α 為通道從關閉到開放的速率，β 為通道從開放到關閉的速率。

${{({{K}_{v}})}_{closed}}{\underset {\beta }{\overset {\alpha }{\longleftrightarrow }}}{{({{K}_{v}})}_{open}}$

由於 n 是通道處於開放狀態的機率，因此通道處於關閉狀態的機率必須為 (1-n)，因為所有通道都處於開放或關閉狀態。因此，通道構象的變化可以用以下公式描述：

${\frac {dn}{dt}}=(1-n)\alpha -n\beta =\alpha -(\alpha +\beta )n$

注意，α 和 β 與電壓有關！霍奇金和赫胥黎在 1952 年使用一種稱為“電壓鉗位”的技術確定了這些速率，他們得出了類似以下的結果：

${\begin{aligned}\alpha (V)&={\frac {0.01*\left(V+10\right)}{\exp \left({\frac {V+10}{10}}\right)-1}}\\\beta (V)&=0.125*\exp \left({\frac {V}{80}}\right)\\\end{aligned}}$

如果您只想模擬電壓依賴性鉀離子通道，這些將是開始使用的方程。（對於電壓門控鈉離子通道，方程稍微複雜一些，因為這些通道具有三種可能的構象：開放、關閉和失活。）

霍奇金-赫胥黎方程

上面提到的電壓門控離子通道的反饋迴路使得確定它們的精確行為變得困難。在第一近似中，動作電位的形狀可以透過分析神經元單個軸突隔室的電路來解釋，該電路由以下元件組成：1）鈉離子通道，2）鉀離子通道，3）氯離子通道，4）洩漏電流，5）膜電容，

原始霍奇金-赫胥黎模型中的最終方程，其中氯離子和其它洩漏電流的電流被組合在一起，如下所示：

${{C}_{m}}{\frac {dV}{dt}}={{G}_{Na}}{{m}^{3}}h({{E}_{Na}}-V)+{{G}_{K}}{{n}^{4}}({{E}_{K}}-V)+{{G}_{m}}({{V}_{rest}}-V)+{{I}_{inj}}(t)$

霍奇金-赫胥黎模型的脈衝行為。

其中$m$、$h$ 和 $n$ 是時間和電壓相關的函式，描述了膜的滲透性。例如，對於鉀離子通道，n 服從上述方程，這些方程是透過電壓鉗位實驗確定的。這些方程能夠高精度地描述動作電位的形狀和傳播！該模型可以使用開源工具輕鬆求解，例如 Python 動態系統工具箱 PyDSTools。一個簡單的求解檔案可在 中找到，輸出結果如下所示。

霍奇金-赫胥黎模型完整連結

• http://fodorwebsite.appspot.com//HHModel.htm

動作電位產生的建模：菲茨休-南摩模型

菲茨休-南摩模型的相平面圖，其中 (a=0.7, b=0.8, c=3.0, I=-0.4)。顯示了四個不同初始條件下的解。虛線表示零斜率線，“o”表示模型的固定點。I=-0.2 將是低於閾值的刺激，導致穩定狀態。而 I=-1.6 將使神經元超極化，也導致一個不同的穩定狀態。

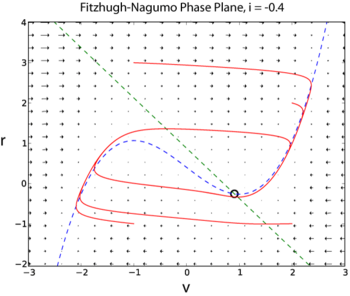
霍奇金-赫胥黎模型有四個動力學變數：電壓$V$，鉀離子通道開啟的機率 $n(V)$，鈉離子通道在之前處於關閉狀態下開啟的機率 $m(V)$，以及鈉離子通道在之前處於失活狀態下開啟的機率 $h(V)$。神經元動作電位產生的簡化模型是菲茨休-南摩 (FN) 模型。與霍奇金-赫胥黎模型不同，FN 模型只有兩個動態變數，透過將變數 $V$ 和 $m$ 組合成單個變數 $v$，並將變數 $n$ 和 $h$ 組合成單個變數 $r$。

${\begin{aligned}&{\frac {dv}{dt}}=c(v-{\frac {1}{3}}{{v}^{3}}+r+I)\\&{\frac {dr}{dt}}=-{\frac {1}{c}}(v-a+br)\end{aligned}}$ 下面的兩個例子取自 I 是注入神經元的外部電流。由於 FN 模型只有兩個動態變數，因此可以使用相平面方法探索其完整動力學（此處提供 Python 中的示例解決方案 ）。

模擬具有正反饋的單個神經元

以下兩個例子取自。這本書提供了對簡單神經系統建模的精彩介紹，並對底層資訊處理有了很好的理解。

讓我們首先看一下單個神經元的響應，其輸入為$x(t)$，並對其自身進行反饋。輸入的權重為$v$，反饋的權重為$w$。神經元的響應$y(t)$由下式給出

$y(t)=wy(t-1)+vx(t-1)$

這表明即使是非常簡單的模擬也可以捕捉到真實神經元的訊號處理特性。

系統對輸入脈衝的輸出：一個“洩漏積分器”

""" Simulation of the effect of feedback on a single neuron """

import numpy as np
import matplotlib.pylab as plt

# System configuration
is_impulse = True   # 'True' for impulse, 'False' for step
t_start = 11        # set a start time for the input     
n_steps = 100       
v = 1               # input weight
w = 0.95            # feedback weight

# Stimulus
x = np.zeros(n_steps)
if is_impulse:     
    x[t_start] = 1  # then set the input at only one time point
else:               
    x[t_start:] = 1 # step input
    
# Response
y = np.zeros(n_steps)           # allocate output vector 
for t in range(1, n_steps):     # at every time step (skipping first) 
    y[t] = w*y[t-1] + v*x[t-1]  # compute the output 

# Plot the results
time = np.arange(n_steps)
fig, axs = plt.subplots(2, 1, sharex=True)

axs[0].plot(time, x)
axs[0].set_ylabel('Input')
axs[0].margins(x=0)

axs[1].plot(time, y)
axs[1].set_xlabel('Time Step')
axs[1].set_ylabel('Output')

plt.show()

模擬一個簡單的神經系統

即使是非常簡單的神經系統，也可以表現出一套令人驚訝的多樣化的行為。一個例子是威爾遜的蝗蟲飛行中央模式發生器模型。這裡系統由下式描述：

${\vec {y}}(t)=\mathbf {W} \cdot {\vec {y}}(t-1)+{\vec {v}}\,x(t-1)$

W 是描述神經元遞迴連線的連線矩陣，並描述了系統的輸入。

輸入 x 以權重 vi 連線到單元 yi (i=1,2,3,4)，單元 y_l (l = 1,2,3,4) 以權重 w_kl 連線到單元 y_k (k = 1,2,3,4)。為了清晰起見，未顯示 y2 和 y3 的自連線，並且未標記各個前饋和遞迴權重。基於 Tom Anastasio 優秀的著作“神經系統建模教程”。

在威爾遜的蝗蟲飛行中央模式發生器 (CPG) 模型的線性版本中，代表運動神經元的單元的響應：一個簡單的輸入脈衝會在神經元 2 和 3 中引發持續的拮抗振盪。

""" 'Recurrent' feedback in simple network:
linear version of Wilson's locust flight central pattern generator (CPG) """

import numpy as np
import matplotlib.pylab as plt

# System configuration
v = np.zeros(4)                     # input weight matrix (vector)
v[1] = 1

w1 = [  0.9,  0.2,    0,     0]     # feedback weights to unit one
w2 = [-0.95,  0.4, -0.5,     0]     # ... to unit two
w3 = [    0, -0.5,  0.4, -0.95]     # ... to unit three
w4 = [    0,    0,  0.2,  0.9 ]     # ... to unit four
W = np.vstack( [w1, w2, w3, w4] )   

n_steps = 100              

# Initial kick, to start the system
x = np.zeros(n_steps)               # zero input vector
t_kick = 11                
x[t_kick] = 1              

# Simulation
y = np.zeros( (4,n_steps) )         # zero output vector
for t in range(1,n_steps):          # for each time step
    y[:,t] = W @ y[:,t-1] + v * x[t-1]  # compute output

# Show the result
time = np.arange(n_steps)     
plt.plot(time, x, '-', label='Input')
plt.plot(time, y[1,:], ls='dashed', label = 'Left Motorneuron')
plt.plot(time, y[2,:], ls='dotted', label='Right Motorneuron')

# Format the plot
plt.xlabel('Time Step')
plt.ylabel('Input and Unit Responses')
plt.gca().margins(x=0)
plt.tight_layout()
plt.legend()
plt.show()

神經形態電路的開發和理論

引言

神經形態工程使用超大規模整合 (VLSI) 系統來構建模擬和數位電路，模擬神經生物學架構和行為。大多數現代電路主要利用數位電路元件，因為它們速度快、精度高且不受噪聲影響。與更符合生物學相關的類比電路不同，數位電路需要更高的電源，並且無法進行平行計算。生物神經元的行為，例如膜洩漏和閾值約束，是材料基底引數的函式，需要模擬系統來建模和微調，而不僅僅是數字 0/1。本文將簡要總結此類神經形態電路及其類比電路元件背後的理論。

神經形態工程的現狀

在過去的 10 年中，神經形態工程領域經歷了快速發展，並受到媒體和科學界的廣泛關注。

在這一話題引起歐盟委員會關注後，人類大腦計劃於 2013 年啟動，並在十年內獲得 6 億歐元的資助。該專案的目標是從分子和神經元水平到神經迴路模擬人腦。它計劃於 2023 年 9 月結束，雖然主要目標尚未實現，但它正在提供至少 200 個大腦區域的詳細 3D 地圖和超級計算機，以模擬記憶和意識等功能，等等。另一個主要成果是於 2019 年推出的EBRAINS虛擬平臺。它提供了一套工具和影像資料，全球科學家可以使用這些工具和資料進行模擬和數字實驗。

同樣在 2013 年，美國國立衛生研究院宣佈為旨在重建大量神經元活動的大腦計劃提供資金。該專案正在進行中，並已撥款 6.8 億美元用於 2023 年之前的研究。

近年來取得的其他主要成就列在下面

1. TrueNorth 晶片 (IBM, 2014)：擁有總共 2.68 億個可程式設計突觸

2. Loihi 晶片 (英特爾, 2017)：基於非同步神經脈衝網路 (SNN) 進行自適應事件驅動平行計算。它在 2021 年被 Loihi2 取代。

3. 原型晶片 (IMEC, 2017)：第一個基於 OxRAM 技術的自學習神經形態晶片

4. Akida AI 處理器開發套件 (Brainchip, 2021)：第一個商用神經形態處理器

電晶體結構與物理

金氧半導體場效應電晶體 (MOSFET) 是現代積體電路的常用元件。MOSFET 被歸類為單極性器件，因為每個電晶體僅使用一種載流子型別；負型 MOFET (nFET) 以電子作為載流子，正型 MOSFET (pFET) 以空穴作為載流子。

n 型 MOSFET 的橫截面。顯示柵極 (G)、體 (B)、源極 (S) 和漏極 (D) 的電晶體。正電流從 n+ 漏極阱流向 n+ 源極阱。來源：維基百科

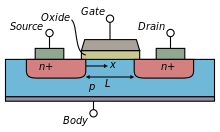
一般的 MOSFET 具有金屬柵極 (G) 和兩個稱為源極 (S) 和漏極 (D) 的 pn 結二極體，如圖 \ref{fig: transistor} 所示。有一個絕緣氧化層將柵極與矽體 (B) 隔開。承載電荷的溝道直接位於該氧化層下方。電流是柵極尺寸的函式。

源極和漏極是對稱的，唯一的區別在於施加在其上的偏置電壓。在nFET器件中，形成源極和漏極的阱是n型，並位於p型襯底中。襯底透過體p型阱接觸進行偏置。正電流在柵極下方的溝道中從漏極流向源極。源極之所以被稱為源極，是因為它是電子的來源。相反，在pFET器件中，p型源極和漏極位於p型襯底中的體n阱中；電流從源極流向漏極。

當載流子由於濃度梯度而移動時，這稱為擴散。如果載流子由於電場而被掃過，則稱為漂移。按照慣例，nFET的漏極偏置電壓高於源極，而pFET的源極偏置電壓更高。

在nFET中，當在柵極上施加正電壓時，正電荷會在金屬觸點上積累。這會將電子從體矽吸引到矽氧化物介面，在源極和漏極之間形成一個帶負電的溝道。柵極電壓越大，溝道越厚，從而降低內部電阻，並因此對數地增加電流。對於小的柵極電壓，通常低於閾值電壓，$V_{th}=0.7V$，溝道尚未完全導通，並且從漏極到源極的電流增加在對數尺度上呈線性增加。當$V_{gs}<V_{th}$時，此狀態稱為亞閾值區。超過此閾值電壓，$V_{gs}>V_{th}$，溝道在源極和漏極之間完全導通，電流處於超閾值區。

電晶體電流作為$V_{g}$的函式，對於$V_{ds}$的固定值。

為了使電流從漏極流向源極，最初必須存在一個電場來將載流子掃過溝道。該電場的強度是源極和漏極之間施加的電位差($V_{ds}$)的函式，因此控制漏極-源極電流。對於$V_{ds}$的小值，電流作為$V_{ds}$的函式呈線性增加，對於恆定的$V_{gs}$值。隨著$V_{ds}$增加超過$100mV$，電流開始飽和。

pFET的行為與nFET類似，只是載流子是空穴，並且接觸偏置被反轉。

在數字應用中，電晶體要麼在其飽和區（導通）工作，要麼處於截止狀態。導通和截止模式之間電位差的這種大範圍是數位電路功耗如此高的原因。相反，類比電路利用電晶體的線性區域來產生連續訊號，並降低功耗。但是，由於柵極或漏極-源極電壓的微小變化會導致電流發生較大變化，因此模擬系統容易受到噪聲的影響。

神經形態工程領域利用類比電路的噪聲特性來複制隨機神經元行為 。與時鐘驅動的數位電路不同，類比電路能夠產生具有與生物時間尺度（約$10\mu sec$）相似的時域動態的動作電位。透過洩漏偏置和可變電阻電晶體延長時間常數來減慢電位並控制放電率。已經建立了能夠模擬具有不同時域動態的生物動作電位的類比電路，從而允許矽電路模擬神經元的基於脈衝的學習行為。而數位電路只能包含二進位制突觸權重[0,1]，類比電路能夠在連續的值範圍內保持突觸權重，這使得類比電路在神經形態電路中特別有利。

基本靜態電路

在理解了電晶體的工作原理和偏置方式後，可以透過這些知識來理解基本的靜態類比電路。之後，這些基本的靜態電路將被組合起來建立神經形態電路。在以下電路示例中，源極、漏極和柵極電壓是固定的，電流是輸出。在實踐中，偏置柵極電壓被固定到亞閾值($0<V_{g}<0.7V$)，漏極保持在飽和狀態($V_{d}>100mV$)，源極和體極接地($V_{s}$，$V_{b}=0V$)。所有非理想特性都被忽略。

基本的靜態電路。(A) 二極體連線的電晶體。(B) 電流鏡。(C) 源極跟隨器。(D) 反相器。(E) 電流傳送器。(F) 差分對。

二極體連線的電晶體

一個二極體連線的nFET將其柵極連線到漏極。由於浮動漏極控制著柵極電壓，漏極-柵極電壓將自動調節，因此器件將始終吸收輸入電流，$I_{ds}$。超過幾個微伏，電晶體將執行在飽和狀態。類似地，一個二極體連線的pFET將其柵極連線到源極。儘管這個簡單的器件似乎僅僅起到了短路的作用，但它通常用於類比電路中複製和調節電流。特別是在神經形態電路中，它們被用來減緩電流吸收，以將電路時間常數增加到生物學上合理的時間範圍。

電流鏡

電流鏡利用了二極體連線的電晶體吸收電流的能力。當輸入電流被迫透過二極體連線的電晶體，$M1$，浮動漏極和柵極被調節到合適的電壓，允許輸入電流透過。由於這兩個電晶體共享一個公共柵極節點，$M2$也將吸收相同的電流。這迫使輸出電晶體複製輸入電流。只要

1. $V_{s1}=V_{s2}$
   
2. ${\frac {W_{M1}}{L_{M1}}}={\frac {W_{M2}}{L_{M2}}}$.
   

輸出電晶體將映象輸入電流。可以透過調整這兩個引數來控制電流鏡的增益。當使用具有不同尺寸的電晶體時，也稱為傾斜鏡，增益為

$Gain={\frac {({\frac {W}{L}})_{M2}}{({\frac {W}{L}})_{M1}}}.$

pFET電流鏡只是翻轉的nFET電流鏡，其中二極體連線的pFET映象輸入電流，並迫使另一個pFET輸出電流。

電流鏡通常用於複製電流而不會消耗輸入電流。這對於反饋迴路尤其重要，例如用於加速動作電位的迴路，以及在突觸處對輸入電流求和。

源極跟隨器

源跟隨器由一個輸入電晶體 $M_{1}$ 和一個疊加在其上的偏置電晶體 $M_{b}$ 組成。固定的亞閾值 ($<0.7V$) 偏置電壓控制著柵極 $M_{b}$，迫使其吸收恆定電流 $I_{b}$。因此，$M_{1}$ 也被強制吸收相同的電流 ($I_{1}=I_{b}$)，而不管輸入電壓 $V_{in}$ 是什麼。

源跟隨器之所以被稱為源跟隨器，是因為輸出 $V_{out}$ 將跟隨 $V_{in}$，並存在由以下公式描述的輕微偏移：

$V_{out}=\kappa \cdot (V_{in}-V_{b}),$
其中 kappa 是亞閾值斜率因子，通常小於 1。

這個簡單的電路通常用作緩衝器。由於電流無法透過柵極，因此該電路不會從輸入端汲取電流，這對低功耗電路來說是一個重要的特性。源跟隨器還可以隔離電路，保護它們免受電源浪湧或靜電的影響。pFET 源跟隨器與 nFET 源跟隨器的唯一區別在於，偏置 pFET 的體連線到 $V_{out}$。

在神經形態電路中，源跟隨器等被用作簡單的電流積分器，其行為類似於突觸後神經元，收集來自許多突觸前神經元的電流。

反相器

一個反相器由一個pFET，$M_{1}$，疊加在一個nFET，$M_{2}$，上構成，它們的柵極連線到輸入端，$V_{in}$，輸出端連線到共源節點，$V_{out}$。當輸入高電平訊號時，pFET關閉但nFET導通，有效地將輸出節點，$V_{out}$，放電，並反相訊號。相反，當輸入訊號為低電平時，nFET關閉但pFET導通，給$V_{out}$節點充電。

這個簡單的電路可以用作快速開關。反相器也常被用作緩衝器，因為它可以產生輸出電流而無需直接提供輸入電流，因為不允許電流透過柵極。當兩個反相器串聯使用時，它們可以用作同相放大器。Mead 等人在 1989 年最初的積分-觸發矽神經元中使用了這種方法，以產生類似於生物動作電位的快速去極化尖峰。然而，當輸入在高低訊號之間波動時，兩個電晶體都處於超閾值飽和狀態，消耗電流，這使得該電路非常耗電。

電流傳送器

電流傳送器也常被稱為緩衝電流映象。電流傳送器由兩個電晶體組成，它們的柵極連線到對方的節點，電流傳送器可以自我調節，使輸出電流與輸入電流匹配，其方式類似於電流映象。

電流傳送器通常用於取代大型串聯重複陣列中的電流映象。這是因為電流映象電流透過柵極控制，柵極的氧化物電容會導致輸出延遲。雖然對於單個輸出電流映象來說，這種延遲可以忽略不計，但對於較長的映象陣列，累積的輸出延遲會很大。這種延遲會極大地阻礙大型並行過程，例如試圖模擬生物神經網路計算策略的過程。

差分對

差分對是一個比較電路，由兩個共源跟隨器和一個公共偏置組成，該偏置強制較弱輸入的電流被抑制。偏置電晶體將強制$I_{b}$保持恆定，將公共節點，$V_{s}$，連線到固定電壓。兩個輸入電晶體都希望分別與其輸入電壓成比例地汲取電流，$I_{1}$和$I_{2}$。但是，由於公共節點必須保持固定，因此輸入電晶體的漏極必須與其柵極電壓成比例地升高。輸入電壓較低的電晶體將充當阻尼器，並減少透過其漏極的電流。輸掉的電晶體將看到其源極電壓增加，因此退出飽和狀態。

在神經元電路的設定中，差分對可以作為離子通道的啟用閾值，低於該閾值，電壓門控離子通道將不會開啟，從而防止神經元產生尖峰。

矽神經元

勝者為王

勝者為王 (WTA) 電路最初由 Lazzaro 等人設計，是一個連續時間類比電路。它比較一組單元的輸出，並且只允許輸出電流最大的單元開啟，抑制所有其他競爭單元。

一個雙輸入 CMOS 勝者為王電路

每個單元包含一個電流控制的傳送器，接收輸入電流，並輸出到控制偏置電晶體的公共線上。輸入電流最大的單元也將輸出最大的電流，從而提高公共節點的電壓。這迫使較弱的單元關閉。WTA 電路可以擴充套件到包含一個大型的競爭單元網路。軟 WTA 也將其輸出電流映象回輸入端，有效地提高單元增益。如果單元陣列的動態範圍較小，則需要這樣做以減少噪聲和隨機切換。

WTA 網路通常用作計算神經網路中競爭學習的一種形式，涉及分散式決策。特別是，WTA 網路已被用於執行低階識別和分類任務，這些任務更類似於視覺選擇任務期間皮層活動。

積分-發放神經元

積分-發放神經元的通用示意圖，也稱為軸突丘神經元，是最常用的脈衝神經元模型。大多數軸突丘電路之間的共同元素包括：具有膜電位$V_{c}$記憶的節點、放大器、正反饋迴路$C_{f}$和將膜電位重置到其靜息狀態的機制$V_{p}$。

輸入電流$I_{i}$為$V_{c}$充電，後者儲存在電容器 C 中。該電容器類似於脂質細胞膜，脂質細胞膜阻止離子的自由擴散，從而在脂質膜兩側積累的電荷差產生膜電位。輸入被放大以輸出電壓尖峰。膜電位的變化透過$C_{f}$正反饋到$V_{c}$，產生更快的尖峰。這與生物軸突丘非常相似，軸突丘密集地填充了電壓門控鈉通道，放大總和電位以產生動作電位。當產生電壓尖峰時，復位偏置$V_{p}$開始耗盡$V_{c}$節點。這類似於鈉鉀通道，鈉鉀通道主動地逆濃度梯度泵送鈉離子和鉀離子以維持靜息膜電位。

脈衝神經元電路。放大器由兩個反相放大器組成，它們產生動作電位特徵性的快速向上擺動。輸出尖峰$V_{o}$由輸入電流$I_{i}$啟動，其寬度由$V_{p}$調製。來源：改編自 Mead 等人，1989 年

DPI 神經元電路。（A）電路示意圖。輸入 DPI 低通濾波器（黃色，ML1-ML3）模擬神經元的洩漏電導。尖峰事件生成放大器（紅色，MA1-MA6）實現基於電流的正反饋（模擬鈉啟用和失活電導），並在極低功耗下產生地址事件。復位塊（藍色，MR1-MR6）復位神經元，並在由 Vref 偏置電壓設定的難治期內保持其處於復位狀態。一個額外的 DPI 濾波器整合尖峰併產生緩慢的超極化電流 Ig，該電流負責尖峰頻率適應（綠色，MG1-MG6）。（B）DPI 神經元電路對恆定輸入電流的響應。測量資料擬合了一個函式，該函式包括在刺激開始時的指數∝e−t/τK，這是所有基於電導的模型的特徵，以及在尖峰開始時的附加指數∝e+t/τNa（基於指數 I&F 計算模型的特徵；Brette 和 Gerstner，2005）。來源：Indiveri 等人，2010 年。

最初的軸突丘矽神經元已經過改進，透過新增一個比較輸入與設定閾值偏置的差分對，從而包含了一個啟用閾值。這種基於電導的矽神經元利用帶洩漏電晶體的差分對積分器（DPI）來比較輸入，$I_{in}$與閾值$V_{thr}$。洩漏偏置$V_{tau}$、不應期偏置$V_{rfr}$、適應偏置$V_{ahp}$和正反饋增益都獨立控制著脈衝頻率。研究一直集中在實現脈衝頻率適應以設定不應期和調節閾值。適應允許神經元將其輸出放電率調節為其輸入的函式。如果存在持續的高頻輸入，神經元將對輸入變得不敏感，並且輸出將隨著時間的推移而逐漸減弱。基於電導的神經元電路的適應元件透過鈣通量建模，並透過適應電容$C_{ahp}$儲存過去活動的資訊。脈衝頻率適應的出現使得神經元層面的變化能夠控制突觸層面的自適應學習機制。這種神經元學習模型是從生物學中建模的，並在矽突觸中進一步討論。

（A）電流衰減機制。（B）作為$V_{mem}$（藍色）函式的自適應閾值機制。神經元的脈衝閾值（紅色）隨著每次脈衝而增加，從而增加了脈衝時間常數。來源：Indiveri 等人，2010 年

矽突觸

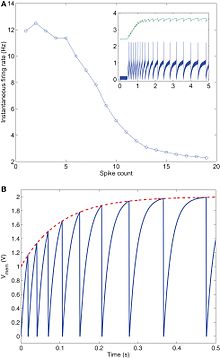
最基本的矽突觸，最初由 Mead 等人於 1989 年使用，僅由一個 pFET 源跟隨器組成，該跟隨器接收低訊號脈衝輸入並輸出單向電流，$I_{o}$。

（A）基本突觸電路。（B）具有更長時間常數的突觸電路。來源：分別改編自 Mead 等人，1989 年和 Lazzaro 等人，1993 年。

脈衝的幅度由權重偏置$V_{w}$控制，脈衝寬度與輸入脈衝寬度直接相關，輸入脈衝寬度由 $V_{\tau}$ 設定。在 Lazzaro 等人（1993 年）的突觸電路中添加了電容器以將脈衝時間常數增加到生物學上合理的值。這減緩了脈衝超極化和去極化的速率，並且是電容的函式。

基本突觸電路。來源：改編自 Lazzaro 等人，1992 年

對於描繪競爭性興奮和抑制行為的多個輸入，對數域積分器使用$I_{1}$和$I_{2}$來調節輸出電流幅度$I_{o}$，作為輸入電流$I_{i}$的函式，根據

$I_{o}=I_{i}\cdot {\sqrt {\frac {I_{1}}{I_{2}}}}.$

$I_{1}$ 控制著 $I_{i}$ 為輸出電晶體柵極充電的速度。 $I_{2}$ 控制著輸出 $I_{o}$ 吸收電流的速度。這種競爭特性對於模擬神經遞質促進或抑制神經元放電的生物學行為是必要的。

突觸模型也已開發出使用對數域濾波器的二階線性積分器，能夠模擬興奮性突觸後電流 (EPSC) 的指數衰減。這對於獲得生物學上合理的脈衝輪廓和時間常數是必要的。增益也可以獨立於突觸時間常數進行控制，這對於脈衝速率和脈衝定時相關的學習機制是必要的。

A) 差分對積分器 (對數域) 突觸的 EPSC（“興奮性突觸後電流”）測量。B) 所用電路的示意圖。（基於 Giacomo Indiveri 的影像）

上述突觸只是簡單地傳遞來自突觸前源的電流，同時改變脈衝尖峰的形狀。然而，它們不包含任何先前尖峰的記憶，也不能夠根據時間動態來適應其行為。但是，如果神經形態電路要像生物神經網路一樣學習，這些能力是必要的。

一個人工神經網路。有 $p$ 個突觸前神經元（$x$），和 $q$ 個突觸後神經元（$b$）。$x_{p}$ 是一個突觸前神經元，它與突觸後神經元 $b_{q}$ 突觸連線，突觸權重為 $w_{pq}$，導致突觸後神經元輸出 $y_{q}$。來源：維基百科

根據赫布法則，學習和記憶等行為被假設發生在突觸水平。它將學習過程歸因於長期的神經元適應，其中突觸前和突觸後的貢獻透過生化修飾得到增強或減弱。該理論通常總結為一句諺語：“一起放電的神經元，會形成連線”。人工神經網路透過這些生化“連線”的修改來模擬學習，使用一個引數，即突觸權重 $w_{pq}$。突觸權重是一個引數狀態變數，它量化了突觸前神經元的脈衝如何影響突觸後神經元的輸出。赫布突觸權重可塑性的兩種模型包括脈衝速率依賴性可塑性 (SRDP) 和脈衝定時依賴性可塑性 (STDP)。自從該理論提出以來，生物神經元的活動已被證明表現出與赫布學習非常相似的行為。一個例子是突觸 NMDA 和 AMPA 受體可塑性修飾，導致鈣通量誘導的適應。

生物神經元中資訊的學習和長期記憶歸因於 NMDA 通道誘導的適應。這些 NMDA 受體是電壓依賴性的，並且控制細胞內鈣離子的通量。動物研究表明，當細胞外鈣減少時，神經元脫敏會減少。

（A）包含 AMPA 和 NMDA 通道以及鈣的簡單突觸。（B）突觸各個元件的電路模型。（C）響應突觸前動作 (AP) 電位輸入 ($AP_{PRE}$）的電路輸出。來源：Rachmuth 等人，2011 年

由於鈣離子濃度呈指數衰減，因此這種行為很容易使用亞閾值電晶體在硬體上實現。Rachmuth 等人（2011）展示了一個演示鈣依賴性生物行為的電路模型。鈣訊號，$I_{Ca_{2+}}$，透過$V_{mem}$節點根據鈣依賴性 STDP 和 SRDP 學習規則調節 AMPA 和 NMDA 通道的活性。這些學習規則的輸出是突觸權重，$w$，它與活躍的 AMPA 和 NMDA 通道的數量成正比。SRDP 模型根據兩個狀態變數$\Omega$（控制更新規則）和$\eta$（控制學習率）來描述權重。

$dw=\eta ([Ca_{2+}])\cdot (\Omega ([Ca_{2+}])-\lambda w),$
其中$w$是突觸權重，$\Omega ([Ca_{2+}])$是更新規則，$\eta ([Ca_{2+}])$是學習率，$\lambda$是一個常數，它允許權重在沒有輸入的情況下漂移出飽和狀態。

NMDA 通道控制鈣離子內流，$I_{Ca}$。NMDA 受體的電壓依賴性由$V_{mem}$建模，並且通道機制由一個大型電容器控制，以增加鈣離子時間常數$\tau _{Ca}$。輸出$I_{Ca}$透過電流映象複製到$\Omega$和$\eta$電路中，以執行下游學習功能。

Ω電路將ICa與閾值偏置（θLTP和θLTD）進行比較，這些偏置分別透過一系列差分對電路控制長期增強或長期抑制。差分對的輸出決定更新規則。該Ω電路已被證明可以展現出海馬體中觀察到的各種Hebbian學習規則，以及小腦中使用的反Hebbian學習規則。

η電路透過僅在ICa高於差分對設定的閾值θη時才允許更新，來控制突觸學習何時發生。學習率（LR）根據以下公式建模：

$\tau _{LR}\sim {\frac {\theta _{\eta }\cdot C_{\eta }}{I_{\eta }\cdot [Ca_{2+}]}},$

其中，$\eta$是$[Ca_{2+}]$的函式，並控制學習率；$C_{\eta }$是$\eta$電路的電容，而$\theta _{\eta }$是比較器的閾值電壓。此函式表明，為了模擬SRDT，必須對$\theta _{\eta }$進行偏置以維持較高的$[Ca_{2+}]$。為了在不活動期間將$V_{\eta }$洩漏至$\eta _{REST}$，包含了一個洩漏電流$I_{LEAK}$。

NEURON模擬環境

引言

Neuron是一個模擬環境，您可以使用它來模擬生物和人工神經元以及神經元網路中離子和動作電位的傳播。使用者可以透過定義和連線神經元細胞部分來指定模型幾何形狀，這些部分可以配備各種機制，例如離子通道、鉗位和突觸。為了與NEURON互動，使用者可以使用圖形使用者介面（GUI）或其中一種程式語言hoc（一種具有類似C語法的語言）或Python作為直譯器。GUI包含了大多數常用功能的廣泛選擇，右側的圖中顯示了一個示例螢幕截圖。另一方面，程式語言可用於向模型新增更具體的機制以及用於自動化目的。此外，可以使用程式語言NMODL建立自定義機制，它是MODL的擴充套件，MODL是由NBSR（國家生物醫學模擬資源）開發的模型描述語言。然後可以編譯這些新機制，並透過GUI或直譯器將其新增到模型中。

Neuron最初由杜克大學的John W. Moore與Michael Hines合作開發。目前，眾多研究所和大學將其用於教育和研究目的。有大量資訊可用，包括包含文件的官方網站、NEURON論壇以及各種教程和指南。此外，2006年出版了NEURON的權威參考書，名為“The NEURON Book”。要閱讀以下章節並使用NEURON，建議您具備一些關於神經元生理學的背景知識。關於神經元的一些資訊來源示例包括WikiBook章節或Khan學院高階神經系統生理學章節介紹中的影片。由於本文件並非旨在作為教程，而只是對NEURON中可能性和模型結構的概述，因此我們不會介紹如何使用NEURON執行此處提到的操作的具體命令或細節。有關使用NEURON進行實現的更多實用資訊，我建議您參考下面連結的教程以及官方網頁上的文件。

模型建立

神經元的示意圖。

單細胞幾何

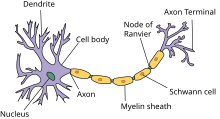
首先，我們將討論建立由單個生物神經元組成的模型幾何形狀。右側的圖中顯示了神經元的示意圖。在下面的清單中，顯示了一個示例程式碼片段，其中使用hoc指定了一個具有一個胞體和兩個樹突的多室細胞。

load_file("nrngui.hoc")

// Create a soma object and an array containing 2 dendrite objects
ndend = 2
create soma, dend[ndend]
access soma

// Initialize the soma and the dendrites
soma {
  nseg = 1
  diam = 18.8
  L = 18.8
  Ra = 123.0
  insert hh
}

dend[0] {
    nseg = 5
    diam = 3.18
    L = 701.9
    Ra = 123
    insert pas
}

dend[1] {
    nseg = 5
    diam = 2.0
    L = 549.1
    Ra = 123
    insert pas
}

// Connect the dendrites to the soma
connect dend[0](0), soma(0)
connect dend[1](0), soma(1)

// Create an electrode in the soma
objectvar stim
stim = new IClamp(0.5)

// Set stimulation parameters delay, duration and amplitude
stim.del = 100
stim.dur = 100
stim.amp = 0.1

// Set the simulation end time
tstop = 300

節段

NEURON 的基本構建塊稱為“段”（sections）。最初，一個段僅表示一個具有個體屬性（例如長度和直徑）的圓柱形管道。透過配備相應的機制，例如離子通道或與其他細胞或人工刺激的突觸連線，一個段可以用來表示不同的神經元部分，例如胞體、樹突或軸突。然後，可以透過以任何你想要的方式連線段的末端來建立神經元細胞，例如樹狀結構，只要沒有迴圈即可。如上所示列表中指定的神經元，在右側的圖中進行了視覺化。

節段（Segments）

為了更準確地模擬動作電位在段中的傳播，可以將段劃分為更小的部分，稱為“節段”（segments）。將段分成多個節段的模型稱為“多室”（multi-compartment）模型。增加節段的數量可以看作是增加了空間離散化的粒度，這在例如膜特性沿段不均勻時會導致更準確的結果。預設情況下，一個段包含一個節段。

膜機制（Membrane Mechanisms）

段的預設設定不包含任何離子通道，但使用者可以新增它們。有兩種型別的內建離子通道膜機制可用，即被動離子通道膜模型和Hodgkin-Huxley 模型膜模型，它表示被動和電壓門控離子通道的組合。如果這還不夠，使用者可以使用 NMODL 程式語言定義自己的膜機制。

點過程（Point Processes）

突觸的示意圖

除了在膜區域定義的膜機制外，還可以向段新增稱為“點過程”（Point processes）的區域性機制。一些示例包括突觸（如右側圖所示）和電壓鉗和電流鉗。同樣，使用者可以使用 NMODL 程式語言自由實現自己的機制。點過程和膜機制之間的一個關鍵區別在於，使用者可以指定應在段上新增點過程的位置，因為它是一種區域性機制。

輸出和視覺化（Output and Visualizations）

可以跟蹤計算量的隨時間變化並進行繪圖，例如建立特定節段內電壓隨時間變化的圖形，如上圖 GUI 螢幕截圖所示。還可以製作動畫，例如顯示軸突內電壓分佈如何隨時間變化。請注意，這些量僅在每個節段的中心和每個段的邊界處計算。

建立細胞網路（Creating a Cell Network）

除了模擬單個細胞內的離子濃度外，還可以連線細胞並模擬神經元網路。為此，使用者必須將突觸（一種點過程）連線到突觸後神經元，然後建立“NetCon”物件，這些物件將充當突觸前神經元和突觸後神經元之間的連線。使用者可以將不同型別的突觸連線到神經元，例如AlphaSynapse，其中突觸電導根據 alpha 函式衰減，以及ExpSyn，其中突觸電導呈指數衰減。與其他機制一樣，也可以使用 NMODL 建立自定義突觸。對於 NetCon 物件，可以指定多個引數，例如閾值和延遲，這些引數決定了突觸前神經元引起突觸後電位的必要條件。

人工神經元（Artificial Neurons）

除了我們迄今為止討論過的生物神經元之外，還有一種可以使用 NEURON 模擬的神經元型別，稱為“人工”（artificial）神經元。NEURON 中生物神經元和人工神經元之間的區別在於，人工神經元沒有空間範圍，並且其動力學高度簡化。NEURON 中有幾個積分器可用於模擬人工細胞的行為，它們的區別在於它們對生物神經元動力學的簡化程度。為了減少人工脈衝神經元細胞和網路模型的計算時間，NEURON 的開發者選擇支援事件驅動模擬。這大大減少了模擬脈衝觸發的突觸傳遞的計算負擔。儘管模擬基於電導的神經元細胞需要連續系統模擬，但 NEURON 仍然可以透過完全支援混合模擬來利用事件驅動方法的優勢，從而模擬包含生物和人工神經元的網路。這樣，任何人工和基於電導的神經元細胞的組合都可以被模擬，同時仍然實現由人工細胞的事件驅動模擬帶來的計算時間減少。使用者還可以使用 NMODL 語言新增其他人工神經元類。

Python 中的 NEURON

Python 徽標

自 1984 年以來，NEURON 一直提供 hoc 直譯器用於建立和執行模擬。hoc 語言已被擴充套件和維護，直到現在一直與 NEURON 一起使用，但由於這種維護需要大量時間，並且事實證明它是一種僅限於 NEURON 使用者的孤立語言，因此 NEURON 的開發者希望使用更現代的程式語言作為 NEURON 的直譯器。由於 Python 在科學計算領域得到廣泛使用，許多使用者建立了包含可重用程式碼的包，因此它現在比 hoc 更具吸引力作為直譯器。有三種方法可以使用 Python 與 NEURON 結合使用。第一種方法是使用終端執行 NEURON，接受互動式 Python 命令。第二種方法是使用直譯器 hoc 執行 NEURON，並透過 hoc 中的特殊命令訪問 Python 命令。第三種方法是將 NEURON 作為 Python 的擴充套件模組使用，以便可以將 NEURON 模組匯入到 Python 或 IPython 指令碼中。

安裝（Installation）

要使用第一種和第二種模式，即使用嵌入式 Python 的 NEURON，只需完成簡單的安裝即可。但是，要使用第三種模式，即作為 Python 擴充套件模組的 NEURON，則需要從原始碼構建 NEURON 並安裝 Python 的 NEURON 共享庫，這在此安裝指南中進行了說明。

Python 中的 NEURON 命令

由於 NEURON 最初是使用 hoc 作為直譯器開發的，因此使用者仍然必須在 Python 中顯式呼叫 hoc 函式和類。在使用嵌入在 NEURON 中的 Python 或使用 NEURON 作為擴充套件模組時，透過“neuron”模組都可以訪問 hoc 中已存在的所有函式和類。hoc 和 Python 中的 NEURON 命令之間只有細微的差別，因此當從一種切換到另一種時，使用者不應該遇到很多複雜情況。與使用 hoc 相比，使用 Python 與 NEURON 結合使用有一些優勢。主要優勢之一是 Python 提供了更多功能，因為它是一種完整的面嚮物件語言，並且有一套廣泛的科學和工程分析工具可用。此外，載入來自 NMODL 指令碼的使用者定義機制變得更容易，這使得 NEURON 對非常具體的機制的模擬更具吸引力。有關 NEURON 與 Python 結合使用的更多詳細資訊，請參見此處。

教程（Tutorials）

您將在第一個教程中學****建模的神經網路的示意圖。藍點表示兩個神經元之間的突觸。

在線上有多個關於NEURON入門教程，下面列出了其中的兩個。

在第一個教程中，您將從學習如何建立一個單隔室細胞開始，並最終建立一個神經元網路，如右側圖所示，其中包含自定義細胞機制。同時，教程將引導您瞭解NEURON的模板、自動化、計算時間最佳化和結果資料提取等功能。該教程使用hoc命令，但Python中的過程幾乎相同。

第二個教程展示瞭如何建立一個具有被動細胞膜和突觸刺激的細胞，以及如何使用Python模組matplotlib視覺化結果。

進一步閱讀

除了本NEURON入門介紹中提到的內容外，還有許多其他選項可供使用，這些選項正在不斷地由開發人員擴充套件和改進。在“NEURON書籍”中可以找到對NEURON的詳細解釋，這是官方參考書。此外，官方網站也包含大量資訊以及其他資源的連結。

參考文獻

另外兩個來源是Chicca等人的“自適應矽突觸”和Liu等人的“模擬VLSI：電路與原理”。