幾何/第 16 章

作圖是指用圓規和直尺來構造圖形（例如正方形、角平分線等）。

構造與給定線段全等的線段

要構造與給定線段全等的線段，將圓規設定到給定線段的兩端點。然後從第二條直線上的一個起點開始，用圓規標記相同的距離。此線段與給定線段全等。

等邊三角形

作圖的一個例子是用兩個相交圓來構造等邊三角形。用相同的半徑繪製兩個圓，使每個圓上的一點與另一個圓的半徑相交。

然後從半徑到兩個圓的交點，以及兩個半徑之間畫線。

現在我們得到了一個等邊三角形。

角平分線

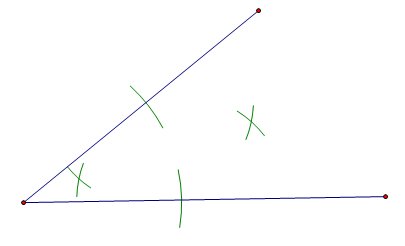
構造角平分線的方法：1. 將圓規的中心放在角上，並在每條線上標記一個交點。

2. 將圓規的中心放在一個標記的交點上，然後在中心附近標記兩個點。在另一個交點上重複此步驟。

3. 畫一條線連線兩個交點和角。

垂直平分線

要構造給定線段 AB 的垂直平分線，首先以點 A 為中心畫一個圓。然後用圓規以點 B 為中心畫一個與第一個圓半徑相同的圓。最後，連線兩個圓的交點，稱為 C 和 D。這條線段就是垂直平分線。推理：任何與線段端點等距的點都位於該線段的垂直平分線上。給出兩個這樣的點，你就可以畫出這條線。

Image:PerpendicularBisector2JPEG.jpg

構造與給定角全等的角

要構造與給定角全等的角，首先在你要構造全等角的線段上畫一條線段。在這條線段上標記一個點，這個點將作為新全等角的頂點。畫一條弧（圓的一部分）穿過原始角的兩邊。然後用與這條弧相同的設定，從線段上的點開始畫一條弧，使這條弧與前一條弧的半徑相同。接下來，用圓規測量第一條弧與角兩邊的交點之間的距離。現在，以相同的設定到第二條弧，在第二條弧上標記與第一條弧相同的距離。將此點與線段上的原始點連線起來。

過直線上一點作這條直線的垂線

給定直線上的一點，首先以該點為中心畫一個圓。用圓與直線的兩個交點畫出兩個全等的弧，它們相互相交。這個點與圓的兩個端點等距，因此在它的垂直平分線上，原始點也一樣。連線這兩個點以完成構造。

過直線外一點作這條直線的垂線

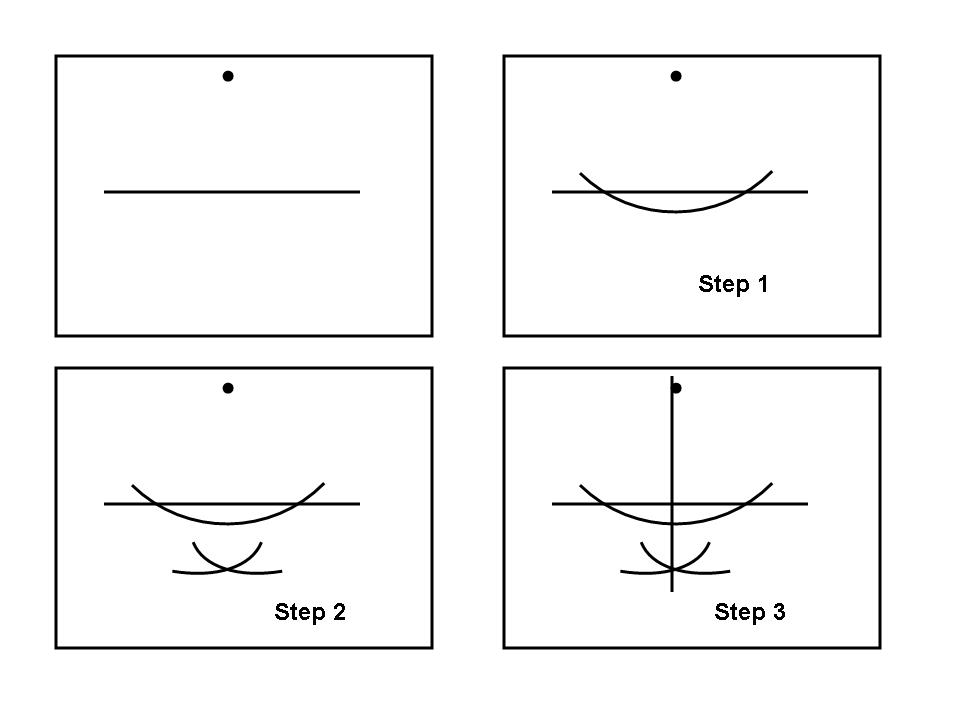
要過直線外一點作這條直線的垂線，以該點為圓心畫一條弧，與直線相交於兩點。你的原始點將位於由這兩個新點形成的線段的垂直平分線上。用這兩個點為中心畫出兩個全等的弧，它們相互相交，你就可以得到該垂直平分線上的另一個點。將這個新點與你的原始點連線起來以完成這個構造。

構造與給定三角形全等的三角形（SSS 方法）

要構造與給定三角形全等的三角形，首先以與構造全等線段相同的方式構造一條底邊。用圓規測量給定三角形的第二邊，然後從構造的線段的一端畫一條弧。將圓規設定為給定三角形的第三邊的長度，然後到構造的線段的第二點，畫出另一條半徑與第三邊相同的弧，與第一條弧相交。將此交點與構造的線段的端點連線起來以完成全等三角形。