幾何/附錄 C

A

銳角

參見 角

等式的代數性質

對於實數 a、b 和 c

加法等式性質：如果 a=b ，則 a+c=b+c

減法等式性質：如果 a=b ，則 a-c+=b-c

乘法等式性質：如果 a=b，則 ac=bc

除法等式性質：如果 a=b 且 c≠0 ，則 (a/c)=(b/c)

對稱等式性質：如果 a=b，則 b=a

傳遞等式性質：如果 a=b 且 b=c ，則 a=c

自反等式性質：如果 a=a ，則 a=a

代入等式性質：如果 a=b，則 a 可以代入 b

分配等式性質：a(b+c)=ab+ac

角

角 ABC 是銳角。

一個圖形是角當且僅當它由兩條具有共同端點的射線組成。每條射線（或線段，視情況而定）被稱為角的邊（例如，${\overline {AB}}\;$在右側的圖示中），共同點被稱為角的頂點（圖示中的點B）。角的度量由它們的斜率差決定。角度量的單位是弧度和度數。角可以按其度數分類。

• 銳角：一個角是銳角當且僅當它的度數小於 90°
• 直角：一個角是直角當且僅當它的度數正好為 90°
• 鈍角：一個角是鈍角當且僅當它的度數大於 90°
• 平角：一個角是平角當且僅當它的度數正好為 180°

使用直角全等定理和平角全等定理，所有直角和所有平角都是全等的。

角加法公理

如果 P 在角 $\angle ABC$ 的內部，則 $\angle ABC=\angle ABP+\angle PBC$

算術平均數

2 個數字 a 和 b 的算術平均數可以計算為：算術平均數=(a+b)/2

B

角平分線

一個圖形平分另一個圖形當且僅當它將它所相交的圖形分成兩個相等的部分。

C

圓心

點P 是圓C 的圓心當且僅當圓C 中的所有點與點P 等距，且點P 與圓C 在同一平面上。

圓

平面上所有與給定點（稱為圓心）等距的點的集合。

周長

圓的周圍距離。

它計算為

C=2πr（其中r是圓的半徑）

餘角

兩個角互餘當且僅當它們的度數之和等於90度。

凹

一個多邊形被稱為凹多邊形當且僅當它至少包含一個內角，其度數大於180°且小於360°。

全等

兩個圖形全等當且僅當它們具有相同的度量。它用“≅”表示。

對應角

有四對對應角：∠1 和 ∠3、∠2 和 ∠4、∠5 和 ∠7、∠6 和 ∠8。

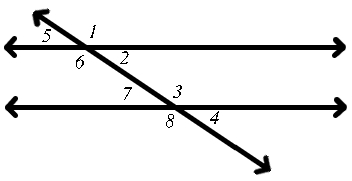
兩條線被一條橫截線所截而形成的兩個角是對應角當且僅當一個角在兩條線的內部，另一個角在兩條線的外部，且它們都在橫截線的同一側。

對應角定理

如果兩條線被一條橫截線所截而平行，那麼它們的對應角全等。

全等三角形的對應邊和對應角全等定理

全等三角形的對應邊和對應角全等定理 (CPCTC) 說明

如果 ∆ABC ≅ ∆XYZ，那麼 ∆ABC 的所有部分都與其在 ∆XYZ 中的對應部分全等。例如

• ${\overline {AB}}\;$ ≅ ${\overline {XY}}\;$

• ${\overline {BC}}\;$ ≅ ${\overline {YZ}}\;$

• ${\overline {AC}}\;$ ≅ ${\overline {XZ}}\;$

• ∠ABC ≅ ∠XYZ

• ∠BCA ≅ ∠YZX

• ∠CAB ≅ ∠ZXY

CPCTC 也適用於三角形的其他所有部分，例如三角形的高、中線、外心等。

餘弦

一個三角函式，縮寫為cos。

cos(θ)=鄰邊/斜邊

D

直徑

一條線段是圓的直徑當且僅當它是一個包含圓心的圓的弦。

參見 圓

距離

兩點之間的距離可以計算為這兩點座標差的絕對值。

在座標系中，點 A(x₁,y₁) 和 B(x₂,y₂) 之間的距離可以計算為

d(AB)=√((y₂-y₁)²+(x₂-x₁)²)

點和線之間的距離透過連線這兩者（使用垂直定理）的垂直線段來衡量。

G

幾何平均數

對於兩個正數 a 和 b，a 和 b 的幾何平均數是滿足 (a/x)=(x/b) 的正數 x。因此，x²=√(ab)

a 和 b 的幾何平均數 = (a/x)=(x/b) : x²=√(ab)

H

平行四邊形的高度

平行四邊形兩底之間的垂直距離

斜邊

在直角三角形中，與直角相對的邊。

利用勾股定理，可以計算斜邊的長度

c²=a²+b²（其中 c 是斜邊，a 和 b 是直角三角形的兩條直角邊）

L

直線

當且僅當點集是完全直的（對齊）、無限長且無限薄時，點集才是一條直線。在線上的任意兩點之間，都存在無限多個也被該直線包含的點。直線通常用直線上兩點來表示，例如直線 AB，或 ${\overleftrightarrow {AB}}$

線段

線段 MN

當且僅當點集是完全直的、無限薄且具有有限長度時，點集才是一條線段。線段的長度由線段上兩個極點（稱為端點）之間的最短距離來衡量。線上段上的任意兩點之間，都存在無限多個也被該線段包含的點。

I

正多邊形的內角

正多邊形的內角都是全等的。因此，具有 n 條邊的正多邊形的一個內角的度數可以計算為

內角 = ((n-2)180)/n

等腰梯形

兩條腰相等的梯形。

等腰三角形

至少有兩條邊相等的三角形。

利用底角定理，與全等邊相對的角也全等。

L

線性對

相鄰的角，其非公共邊是相反射線。

根據線性對公理，線性對中的角也是互補的。

如果構成線性對的兩個角全等，那麼這兩個角都是直角，並且包含這兩個角的直線是垂直的。

M

優弧

度數大於 180 度的弧。它必須由 3 個點命名。

梯形的 中線

連線梯形兩腰中點的線段。

它平行於底邊，其長度是兩底長度的算術平均數。

劣弧

度數小於 180 度的弧。

P

平行線

當且僅當兩條直線或線段被包含在同一個平面上，並且當無限延長時沒有公共點，它們就被稱為平行。

在座標系中，兩條直線平行當且僅當它們具有相同的斜率。

平行平面

當且僅當兩個平面無限延長時沒有公共點，這兩個平面就被稱為平行。

垂直線

在 90° 角處相交的兩條直線。

在座標系中，兩條直線垂直當且僅當它們的斜率之積等於 -1（或它們的斜率是負倒數）。

垂直公理

給定一條直線，${\overleftrightarrow {AB}}$，以及不在直線 ${\overleftrightarrow {AB}}$ 上的點 P，則只有一條直線透過點 P 且垂直於 ${\overleftrightarrow {AB}}$

平面

當且僅當一個物體是二維的、沒有厚度或曲率並無限延伸時，它才是平面。平面可以用三個點來定義。平面可以被認為類似於一張紙[1]。

點

點是一個零維的數學物件，代表一個或多個維度中的位置[2]。點沒有大小；它只有位置。

多邊形

多邊形是由至少 3 條直線組成的封閉平面圖形。每條邊都必須在其各自的端點處與另一條邊相交，並且相交的線不是共線的。

R

半徑

圓的半徑是圓上任意一點到圓心的距離。

同一個圓（或全等圓）的所有半徑具有相同的度量。

參見 圓

射線

射線是一個直線點集，它在一個方向上無限延伸。射線停止的點被稱為射線的端點。在射線上的任意兩點之間，存在無限多個也包含在射線中的點。

正多邊形

正多邊形是等邊且等角的多邊形。

尺規公理

直線上的點可以與實數一一對應。對應於點的實數是該點的座標。兩點之間的距離是兩點座標之差的絕對值。

S

半圓

弧度為 180 度的弧。

多邊形內角和

具有 n 個邊的多邊形的內角和的計算方法為

內角和 = (n-2)180

補角

當且僅當兩個角的度數之和等於 180 度時，這兩個角互為補角。

導航

• 幾何學主頁
• Motivation
• Introduction
• Geometry/Chapter 1 - HS 定義和推理（介紹）
  • Geometry/Chapter 1/Lesson 1 簡介
  • Geometry/Chapter 1/Lesson 2 推理
  • 幾何/第 1 章/第 3 課 未定義術語
  • 幾何/第 1 章/第 4 課 公理/公設
  • 幾何/第 1 章/第 5 課 定理
  • 幾何/第 1 章/詞彙 詞彙
• 幾何/第 2 章 證明
• 幾何/第 3 章 邏輯論證
• 幾何/第 4 章 全等和相似
• 幾何/第 5 章 三角形：全等和相似
• 幾何/第 6 章 三角形：不等式定理
• 幾何/第 7 章 平行線、四邊形和圓
• 幾何/第 8 章 周長、面積、體積
• 幾何/第 9 章 稜柱、稜錐、球體
• 幾何/第 10 章 多邊形
• 幾何/第 11 章 $\mathbb {R} ,\mathbb {R} ^{2},\mathbb {R} ^{3}$
• 幾何/第 12 章 角：內角和外角
• 幾何/第 13 章 角：餘角、補角、對頂角
• 幾何/第 14 章 勾股定理：證明
• 幾何/第 15 章 勾股定理：距離和三角形
• 幾何/第 16 章 作圖
• 幾何/第 17 章 座標幾何
• 幾何/第 18 章 三角學
• 幾何/第 19 章 三角學：解三角形
• 幾何/第 20 章 特殊直角三角形
• 幾何/第 21 章 弦、割線、切線、圓內角、圓外角
• 幾何/第 22 章 剛性運動
• 幾何/附錄 A 公式
• 幾何/附錄 B 問題答案
• 附錄 C. 幾何/公理與定義
• 附錄 D. 幾何/SMSG 歐氏幾何公理