幾何/第 7 章
在歐幾里得幾何中,如果兩條直線不相交,則它們是平行的。
請記住,直線無限延伸,如果它們不平行,它們最終會相交。
畫一條直線 AB,畫一條平行於 AB 的直線 CD
找到一種方法來證明 AB 平行於 CD
在歐幾里得幾何中,如果兩條直線相交成 90 度角,則它們是垂直的。

畫一條直線 AB,然後在直線 AB 上選取一個點 C,畫一條與 C 相交且垂直於 AB 的直線,即
證明直線 CD 垂直於 AB。
全等圓形是指大小相同,即半徑相同的圓形。
同心圓形共享相同的中心、軸或原點,一個在另一個裡面。同心圓形不一定具有相同的半徑。
畫一個圓形,找到一種方法來畫一個全等圓形,證明它們是全等的
畫一個圓形,然後畫一個同心圓形,證明它們是同心圓形。
半徑是連線圓形上一點和圓心的一條線段。
直徑是連線圓形上兩點並穿過圓心的線段。
弦是連線圓形上兩點的線段,它不必穿過圓心。圓形的直徑是最長的弦。
四邊形被定義為任何四邊多邊形。這意味著正方形、矩形等都被稱為四邊形。在以下章節中,我們將仔細研究每個重要的四邊形,它們是如何定義的,以及它們各自的一些特殊屬性。
矩形被定義為具有 4 個條件。第一個是它是一個四邊多邊形。第二個是它有兩對平行邊。第三個是平行邊對的長度相等。第四個是所有角必須等於 90 度或直角。
讓我們舉個例子。下面是一個矩形。首先我們注意到它有 4 條邊,它們形成一個多邊形,這使得它成為一個四邊多邊形,因此滿足了第一個條件。接下來我們注意到 2 條邊彼此平行,另外 2 條邊也彼此平行,因此滿足了第二個條件。現在我們注意到平行邊對的長度相等,因此滿足了第三個條件。最後一個條件是所有角必須是 90 度,如影像所示,它們實際上是 90 度。因為所有 4 個條件都已滿足,我們現在知道下面的多邊形實際上是一個矩形。
好的,現在矩形已經定義好了,我們需要知道矩形有什麼特別之處。
對角線的長度
下面是與上面相同的矩形,只是它有一條從一個頂點到另一個頂點的對角線。這條對角線的長度等於一邊平方加上相鄰邊平方之和的平方根。例如:
這個證明非常簡單。但是首先你必須知道勾股定理,如果你還沒有了解它,請先閱讀一下。
1) ∠ABC = 90 度 - 矩形的定義所給。
2) AB 邊和 BC 邊以及對角線構成一個三角形。- 一個三邊形。
3) 這個三角形也是一個直角三角形,因為它有一個直角。- ∠ABC
4) 矩形的對角線是三角形的斜邊。
5) 直角三角形的斜邊等於兩條直角邊的平方和的平方根 - 勾股定理
6) 因此,對角線等於
根據此特性,我們可以注意到,如果我們畫一條對角線,就會在矩形內建立兩個全等的三角形。
證明
下面是一個畫了對角線的矩形。我們把頂點命名為 A、B、C、D。對角線稱為 AC,因為兩個端點是 A 和 C。兩個三角形是 ABC 和 ADC。

1) 兩個三角形共用一條邊 - AC。
2) AD 和 BC 的長度相等 - 已知。
3) ∠ABC 和 ∠ADC 的度數相等 - 矩形的定義。
4) 每個三角形都有一個度數相等的角 - 語句 3。
5) 根據邊角邊定理,每個三角形都是全等的。
例子
[edit | edit source]正方形
[edit | edit source]正方形具有與矩形相同的性質,只是所有 4 條邊必須長度相等。正方形也被認為是菱形、風箏形、平行四邊形和梯形。
特殊屬性
[edit | edit source]例子
[edit | edit source]梯形
[edit | edit source]梯形是四邊形,其中兩條邊平行。

特殊屬性
[edit | edit source]梯形的面積由以下公式給出:
,其中 a 和 b 是兩條平行邊的長度,h 是高度。
例子
[edit | edit source]<1=
菱形
[edit | edit source]菱形是四邊形,四邊相等。

特殊屬性
[edit | edit source]菱形的面積由以下公式給出:
其中 D1 和 D2 是兩條對角線的長度
因為菱形是平行四邊形,所以面積也等於一條邊的長度 (B) 乘以兩條相對邊之間的垂直距離 (H)
面積也等於邊長的平方乘以任何一個內角的正弦
其中 a 是邊的長度, 是兩條邊之間的角度。
例子
[edit | edit source]平行四邊形
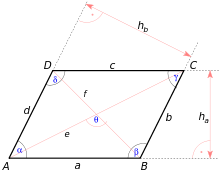
[edit | edit source]平行四邊形是四邊形,有兩組平行邊。
特殊屬性
[edit | edit source]平行四邊形的面積
- 其中 B 是底,H 是高
平行四邊形的對角線互相平分。
例子
[edit | edit source]導航
- 幾何學主頁
- 動機
- 介紹
- 幾何學/第 1 章 - 高中 定義和推理(引言)
- 幾何學/第 1 章/第 1 課 介紹
- 幾何學/第 1 章/第 2 課 推理
- 幾何學/第 1 章/第 3 課 未定義術語
- 幾何學/第 1 章/第 4 課 公理/公設
- 幾何學/第 1 章/第 5 課 定理
- 幾何學/第 1 章/詞彙 詞彙
- 幾何學/第 2 章 證明
- 幾何學/第 3 章 邏輯論證
- 幾何學/第 4 章 全等和相似
- 幾何學/第 5 章 三角形:全等和相似
- 幾何學/第 6 章 三角形:不等式定理
- 幾何學/第 7 章 平行線、四邊形和圓
- 幾何學/第 8 章 周長、面積、體積
- 幾何學/第 9 章 稜柱、稜錐、球體
- 幾何學/第 10 章 多邊形
- 幾何/第 11 章
- 幾何/第 12 章 角:內角和外角
- 幾何/第 13 章 角:餘角、補角、對頂角
- 幾何/第 14 章 勾股定理:證明
- 幾何/第 15 章 勾股定理:距離和三角形
- 幾何/第 16 章 作圖
- 幾何/第 17 章 座標幾何
- 幾何/第 18 章 三角學
- 幾何/第 19 章 三角學:解三角形
- 幾何/第 20 章 特殊直角三角形
- 幾何/第 21 章 弦、割線、切線、圓內角、圓外角
- 幾何/第 22 章 剛性運動
- 幾何/附錄 A 公式
- 幾何/附錄 B 答案
- 附錄 C. 幾何/公理與定義
- 附錄 D. 幾何/SMSG 歐幾里得幾何公理
















