幾何/附錄 C

A

銳角

參見 角

等式代數性質

對於實數 a、b 和 c

加法等式性質：如果 a=b，則 a+c=b+c

減法等式性質：如果 a=b，則 a-c=b-c

乘法等式性質：如果 a=b，則 ac=bc

除法等式性質：如果 a=b 且 c≠0，則 (a/c)=(b/c)

對稱等式性質：如果 a=b，則 b=a

傳遞等式性質：如果 a=b 且 b=c，則 a=c

自反等式性質：如果 a=a，則 a=a

替換等式性質：如果 a=b，則 a 可以用 b 代替

分配等式性質：a(b+c)=ab+ac

角

角 ABC 是銳角。

當且僅當一個圖形由兩條共享一個公共端點的射線組成時，該圖形為一個角。每條射線（或線段，視情況而定）被稱為該角的邊（例如，${\overline {AB}}\;$ 在右邊的插圖中），公共點被稱為角的頂點（在插圖中為點B）。角的測量是透過其斜率之差來衡量的。角的測量單位是弧度和度數。角可以根據其度數進行分類。

• 銳角：當且僅當一個角的度數小於 90° 時，該角為一個銳角
• 直角：當且僅當一個角的度數恰好為 90° 時，該角為一個直角
• 鈍角：當且僅當一個角的度數大於 90° 時，該角為一個鈍角
• 平角：當且僅當一個角的度數恰好為 180° 時，該角為一個平角

根據直角全等定理和平角全等定理，所有直角和所有平角都全等

角加法公理

如果 P 在角 $\angle ABC$ 的內部，則 $\angle ABC=\angle ABP+\angle PBC$

算術平均值

2 個數字 a 和 b 的算術平均值可以計算為：算術平均值 = (a+b)/2

B

角平分線

當且僅當一個圖形將它所相交的圖形分成兩個相等的部分時，該圖形平分另一個圖形

C

圓心

點P 是圓C 的圓心，當且僅當圓C 中的所有點都與點P 等距，並且點P 與圓C 在同一個平面內。

圓

平面中與一個給定點（稱為圓心）等距的所有點的集合。

圓周

圓的周長。

計算公式為

C=2πr（其中r為圓的半徑）

餘角

如果且僅當兩個角的度數之和等於90度，則這兩個角互為餘角。

凹

如果且僅當一個多邊形至少包含一個內角，其度數大於180°且小於360°，則該多邊形被稱為凹多邊形。

全等

如果且僅當兩個圖形具有相同的度量，則這兩個圖形全等。用"≅"表示。

對應角

有四對對應角: ∠1 和 ∠3，∠2 和 ∠4，∠5 和 ∠7，以及 ∠6 和 ∠8。

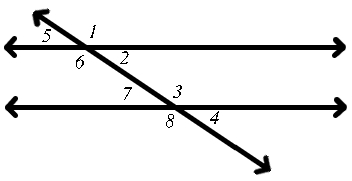
如果且僅當一條橫截線與兩條直線相交形成的兩個角，一個位於兩條直線內部，另一個位於兩條直線外部，且都在橫截線的同一側，則這兩個角互為對應角。

對應角定理

如果兩條直線被一條橫截線所截，則它們之間的對應角相等。

全等三角形的對應邊和對應角相等定理

全等三角形的對應邊和對應角相等定理 (CPCTC) 表明

如果 ∆ABC ≅ ∆XYZ，那麼 ∆ABC 的所有部分都與其在 ∆XYZ 中的對應部分相等。例如

• ${\overline {AB}}\;$ ≅ ${\overline {XY}}\;$

• ${\overline {BC}}\;$ ≅ ${\overline {YZ}}\;$

• ${\overline {AC}}\;$ ≅ ${\overline {XZ}}\;$

• ∠ABC ≅ ∠XYZ

• ∠BCA ≅ ∠YZX

• ∠CAB ≅ ∠ZXY

CPCTC 也適用於三角形的所有其他部分，如三角形的高、中線、外心等。

餘弦

一個三角函式，縮寫為 cos。

cos(θ)=鄰邊/斜邊

D

直徑

如果且僅當一條線段是圓的弦並且包含圓心，則該線段是圓的直徑。

參見 圓

距離

兩點之間的距離可以計算為這兩點座標差的絕對值。

在座標系中，點 A(x₁,y₁) 和 B(x₂,y₂) 之間的距離可以計算為

d(AB)=√((y₂-y₁)²+(x₂-x₁)²)

點和直線之間的距離由連線這兩者的垂直線段測量（使用垂直定理）。

G

幾何平均數

對於兩個正數 a 和 b，a 和 b 的幾何平均數是滿足 (a/x)=(x/b) 的正數 x。因此，x²=√(ab)

a 和 b 的幾何平均數 = (a/x)=(x/b) : x²=√(ab)

H

平行四邊形的高度

平行四邊形兩底之間的垂直距離

斜邊

在直角三角形中，直角所對的邊。

使用勾股定理，斜邊的度量可以計算為

c²=a²=b²（其中 c 為斜邊，a 和 b 為直角三角形的兩條直角邊）

L

線

點集為直線當且僅當點集完全直線（對齊），無限長，無限薄。 在直線上的任意兩點之間，存在無限數量的點也包含在直線中。 直線通常用直線上的兩點表示，例如直線AB，或 ${\overleftrightarrow {AB}}$

線段

線段MN

點集為線段當且僅當它完全直線，無限薄，且具有有限長度。 線段的度量由線段上兩個極端點（稱為端點）之間的最短距離測量。 線上段上的任意兩點之間，存在無限數量的點也包含線上段中。

我

正多邊形的內角

正多邊形的內角都全等。 因此，可以計算出具有n個邊的正多邊形的一個內角的度數

int angle = ((n-2)180)/n

等腰梯形

腰長相等的梯形。

等腰三角形

至少有兩條邊相等的三角形。

利用底角定理，與全等邊相對的角也全等。

L

線性對

非公共邊為相反射線的相鄰角。

利用線性對定理，線性對中的角也互補。

如果構成線性對的兩個角全等，則這兩個角都是直角，且包含這兩個角的直線垂直。

M

優弧

度數大於 180 度的弧。 它必須用 3 個點命名。

梯形的中位線

連線梯形腰中點的線段。

它平行於底，其長度是底長度算術平均值。

劣弧

度數小於 180 度的弧。

P

平行線

兩條直線或線段被稱為平行，當且僅當這些直線包含在同一個平面中，並且如果無限延伸，則它們沒有公共點。

在座標平面上，兩條直線平行當且僅當它們具有相同的斜率。

平行平面

兩條平面被稱為平行，當且僅當這些平面無限延伸時沒有公共點。

垂直線

在 90° 角處相交的兩條直線。

在座標平面上，兩條直線垂直當且僅當它們的斜率的乘積等於 -1（或者如果它們的斜率是負倒數）。

垂直定理

給定一條直線，${\overleftrightarrow {AB}}$ 和一個不在直線 ${\overleftrightarrow {AB}}$ 上的點 P，那麼只有一條直線經過點 P 垂直於 ${\overleftrightarrow {AB}}$

平面

物體為平面當且僅當它是二維物體，沒有厚度或曲率，並且無限延伸。 平面可以用三個點定義。 平面可以被認為類似於一張紙[1].

點

點是一個零維的數學物件，代表著一個或多個維度中的位置[2]。點沒有大小，只有位置。

多邊形

多邊形是一個封閉的平面圖形，由至少 3 條直線組成。每條邊必須在其各自的端點處與另一條邊相交，並且相交的直線不共線。

R

半徑

圓的半徑是圓上任意一點到圓心的距離。

同一個圓（或全等圓）中所有的半徑長度都相同。

參見 圓

射線

射線是由一系列直線點組成的，這些點在一個方向上無限延伸。射線停止的點被稱為射線的端點。在射線上的任意兩個點之間，存在無限多個也包含在射線中的點。

正多邊形

正多邊形是等邊且等角的多邊形。

尺規作圖公理

直線上的點可以與實數一一對應。對應於點的實數是點的座標。兩點之間的距離是這兩點座標之差的絕對值。

S

半圓

度數為 180 度的弧。

多邊形的內角和

一個有 n 條邊的多邊形的內角和的計算公式為：

內角和 = (n-2)180

互補角

當且僅當兩個角的度數之和等於 180 度時，這兩個角互補。

導航

• 幾何學主頁
• 動機
• 簡介
• 幾何學/第一章 - 高中 定義和推理（簡介）
  • 幾何學/第一章/第一節 簡介
  • 幾何學/第一章/第二節 推理
  • 幾何學/第一章/第三節 未定義術語
  • 幾何學/第一章/第四節 公理/公設
  • 幾何學/第一章/第五節 定理
  • 幾何學/第一章/詞彙表 詞彙表
• 幾何學/第二章 證明
• 幾何學/第三章 邏輯論證
• 幾何學/第四章 全等和相似
• Geometry/Chapter 5 三角形：全等與相似
• Geometry/Chapter 6 三角形：不等式定理
• Geometry/Chapter 7 平行線、四邊形和圓形
• Geometry/Chapter 8 周長、面積、體積
• Geometry/Chapter 9 稜柱、稜錐、球體
• Geometry/Chapter 10 多邊形
• Geometry/Chapter 11 $\mathbb {R} ,\mathbb {R} ^{2},\mathbb {R} ^{3}$
• Geometry/Chapter 12 角：內角和外角
• Geometry/Chapter 13 角：餘角、補角、對頂角
• Geometry/Chapter 14 勾股定理：證明
• Geometry/Chapter 15 勾股定理：距離和三角形
• Geometry/Chapter 16 作圖
• Geometry/Chapter 17 解析幾何
• Geometry/Chapter 18 三角函式
• Geometry/Chapter 19 三角函式：解三角形
• Geometry/Chapter 20 特殊直角三角形
• Geometry/Chapter 21 弦、割線、切線、圓周角、外角
• Geometry/Chapter 22 剛性運動
• Geometry/Appendix A 公式
• 幾何/附錄 B 習題答案
• 附錄 C. 幾何/公理和定義
• 附錄 D. 幾何/SMSG 歐幾里得幾何公理