工程聲學/低音反射箱體設計

簡介

低音反射箱體改善了揚聲器系統的低頻響應。低音反射箱體也被稱為“通風箱設計”或“帶埠箱體設計”。低音反射箱體在箱體和周圍環境之間包含一個通風口或埠。這種設計，正如人們從當代揚聲器產品中觀察到的那樣，至今仍在廣泛使用。雖然低音反射箱體的構造相當簡單，但其設計並不簡單，需要適當的調諧。本參考資料側重於低音反射設計的技術細節。有關揚聲器的通用資訊，請點選此處檢視。

埠對箱體響應的影響

在討論低音反射箱體之前，瞭解更簡單的密閉箱體系統效能非常重要。顧名思義，密閉箱體系統將揚聲器連線到一個密閉的箱體（除了包含一個小的洩漏來平衡箱體內部的環境壓力）。理想情況下，箱體將充當聲學順應元件，因為箱體內的空氣被壓縮和稀薄。然而，通常會在箱體內部新增聲學材料以減少駐波，消散熱量以及其他原因。這在聲學集總元件模型中添加了一個電阻元件。箱體效應的非理想模型實際上會新增一個聲學質量元件來完成圖 1 所示的串聯集總元件電路。有關密閉箱體設計的更多資訊，請檢視密閉箱低音炮設計頁面。

圖 1. 密閉箱體聲學電路。

在低音反射箱體的情況下，會在結構中新增一個埠。通常，埠是圓柱形的，並且在指向箱體外部的一端有法蘭。在低音反射箱體中，使用的聲學材料量通常遠少於密閉箱體的情況，通常根本沒有使用。這允許空氣自由流過埠。相反，更大的損失來自箱體中的空氣洩漏。使用這種設定，集總元件聲學電路具有以下形式。

圖 2. 低音反射箱體聲學電路。

在本圖中，$Z_{RAD}$ 表示揚聲器振膜在外部環境中的輻射阻抗。與密封箱體情況相比，振膜背面的負載發生了變化。如果想象一下箱體內部空氣的運動，一些空氣會因箱體的順應性而被壓縮和稀薄，一些空氣會洩漏出箱體，一些空氣會從埠流出。這解釋了$M_{AP}$、$C_{AB}$ 和 $R_{AL}$ 的並聯組合。一個真正現實的模型將把埠的輻射阻抗與 $M_{AP}$ 串聯，但目前忽略它。最後，$M_{AB}$，即箱體的聲學質量，被包含在內，如密封箱體情況中所述。計算箱體引數的公式在附錄 B 中列出。

需要注意 $M_{AP}$ 和 $C_{AB}$ 的並聯組合。這形成了一個亥姆霍茲共振器（點選此處瞭解更多資訊）。從物理上講，埠充當共振器的“頸部”，箱體充當“腔體”。在這種情況下，共振器直接由活塞驅動腔體，而不是典型的亥姆霍茲情況下它在“頸部”驅動。然而，相同的共振行為仍然在箱體共振頻率 $f_{B}$ 發生。在這個頻率下，揚聲器振膜看到的阻抗很大（見下圖 3）。因此，揚聲器上的負載降低了流過其機械引數的速度，導致反共振狀態，其中振膜的位移最小。相反，大多數體積速度實際上是由埠本身發射的，而不是由揚聲器發射的。當此阻抗反射到電路時，它與 $1/Z$ 成正比，因此音圈看到的阻抗的最小值很小。圖 3 顯示了在揚聲器端子處看到的阻抗的曲線圖。在這個例子中，$f_{B}$ 被發現約為 40 Hz，這對應於音圈阻抗中的零點。

圖 3. 揚聲器振膜和音圈看到的阻抗。

埠在箱體上的定量分析

揚聲器的效能首先由其速度響應來衡量，這可以直接從系統的等效電路中得出。由於大多數揚聲器設計的目標是改善低音響應（將高頻生產留給高音喇叭），因此將在分析中儘可能地進行低頻近似以簡化分析。首先，音圈的電感，${\it {L_{E}}}$，只要$\omega \ll R_{E}/L_{E}$，就可以忽略。在典型的揚聲器中，${\it {L_{E}}}$ 大約為 1 mH，而 ${\it {R_{E}}}$ 通常為 8$\Omega$，因此此近似的上限頻率約為 1 kHz，對於感興趣的頻率範圍來說肯定足夠高。

另一個近似涉及輻射阻抗，${\it {Z_{RAD}}}$。可以證明 [1] 此值由以下公式給出（以聲學歐姆為單位）

$Z_{RAD}={\frac {\rho _{0}c}{\pi a^{2}}}\left[\left(1-{\frac {J_{1}(2ka)}{ka}}\right)+j{\frac {H_{1}(2ka)}{ka}}\right]$

其中$J_{1}(x)$ 和 $H_{1}(x)$ 是貝塞爾函式的型別。對於ka 的小值，

$J_{1}(2ka)\approx ka$

以及

$H_{1}(2ka)\approx {\frac {8(ka)^{2}}{3\pi }}$

$\Rightarrow Z_{RAD}\approx j{\frac {8\rho _{0}\omega }{3\pi ^{2}a}}=jM_{A1}$

因此，揚聲器的低頻阻抗用聲學質量表示$M_{A1}$ [1]。為了簡單分析，$R_{E}$，$M_{MD}$，$C_{MS}$ 和 $R_{MS}$（換能器引數或 _Thiele-Small_ 引數）轉換為其聲學等效值。所有引數的所有轉換都在附錄 A 中給出。然後，串聯質量，$M_{AD}$，$M_{A1}$ 和 $M_{AB}$，合併在一起以建立 $M_{AC}$。這個新電路如下所示。

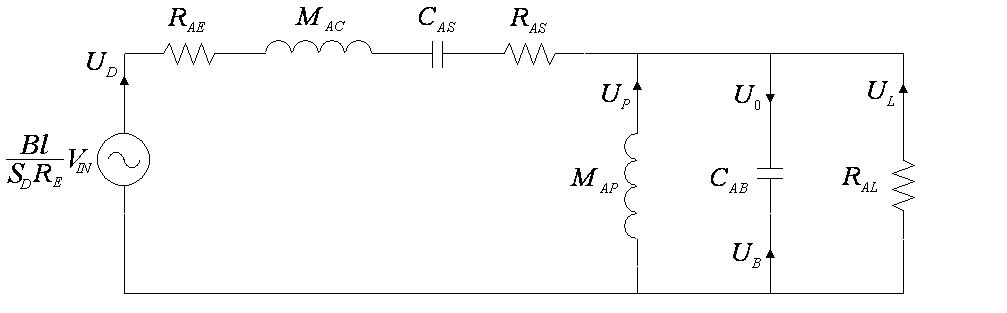
圖 4. 低頻等效聲學電路

與密封箱體分析不同，有多個體積速度源輻射到外部環境。因此，振膜體積速度，$U_{D}$，沒有被分析，而是$U_{0}=U_{D}+U_{P}+U_{L}$。這實際上是在箱體周圍畫了一個“氣泡”，並將系統視為具有體積速度 $U_{0}$ 的源。這種“集中”方法只對低頻有效，但先前的近似值已經將分析限制在這些頻率範圍內。從電路可以看出，流入箱體的體積速度，$U_{B}=-U_{0}$，壓縮了箱體內的空氣。因此，圖 3 的電路模型是有效的，並且可以計算輸入電壓，$V_{IN}$ 與 $U_{0}$ 的關係。

為了使方程式更容易理解，將幾個引數組合起來形成其他引數名稱。首先，$\omega _{B}$ 和 $\omega _{S}$，分別為箱體和揚聲器的諧振頻率，是

$\omega _{B}={\frac {1}{\sqrt {M_{AP}C_{AB}}}}$

$\omega _{S}={\frac {1}{\sqrt {M_{AC}C_{AS}}}}$

基於推導的性質，定義引數 $\omega _{0}$ 和 h，即亥姆霍茲調諧比，是十分方便的。

$\omega _{0}={\sqrt {\omega _{B}\omega _{S}}}$

$h={\frac {\omega _{B}}{\omega _{S}}}$

一個被稱為順應比或體積比的引數，$\alpha$，由下式給出：

$\alpha ={\frac {C_{AS}}{C_{AB}}}={\frac {V_{AS}}{V_{AB}}}$

其他引數被組合成被稱為品質因數的引數。

$Q_{L}=R_{AL}{\sqrt {\frac {C_{AB}}{M_{AP}}}}$

$Q_{TS}={\frac {1}{R_{AE}+R_{AS}}}{\sqrt {\frac {M_{AC}}{C_{AS}}}}$

這種表示法使得最終傳遞函式的表達更加簡潔 [1]。

${\frac {U_{0}}{V_{IN}}}=G(s)={\frac {(s^{3}/\omega _{0}^{4})}{(s/\omega _{0})^{4}+a_{3}(s/\omega _{0})^{3}+a_{2}(s/\omega _{0})^{2}+a_{1}(s/\omega _{0})+1}}$

其中

$a_{1}={\frac {1}{Q_{L}{\sqrt {h}}}}+{\frac {\sqrt {h}}{Q_{TS}}}$

$a_{2}={\frac {\alpha +1}{h}}+h+{\frac {1}{Q_{L}Q_{TS}}}$

$a_{3}={\frac {1}{Q_{TS}{\sqrt {h}}}}+{\frac {\sqrt {h}}{Q_{L}}}$

低頻壓力響應的開發

可以證明 [2]，對於 $ka<1/2$，揚聲器表現為球面聲源。這裡，a 代表揚聲器的半徑。對於空氣中的 15 英寸直徑揚聲器，此低頻限制約為 150 赫茲。對於更小的揚聲器，此限制會增加。此限制主導了忽略 $L_{E}$ 的限制，並且與透過 $M_{A1}$ 對 $Z_{RAD}$ 建模的限制一致。

在此限制範圍內，揚聲器發出體積速度 $U_{0}$，如上一節所述。對於具有體積速度 $U_{0}$ 的簡單球面聲源，遠場壓力由 [1] 給出

$p(r)\simeq j\omega \rho _{0}U_{0}{\frac {e^{-jkr}}{4\pi r}}$

對於此分析，可以簡單地令 $r=1$，而不會損失一般性，因為距離僅是周圍環境的函式，而不是揚聲器的函式。此外，由於傳遞函式幅度是最主要的關注點，因此省略了指數項，該項具有單位幅度。因此，系統的壓力響應由 [1] 給出

${\frac {p}{V_{IN}}}={\frac {\rho _{0}s}{4\pi }}{\frac {U_{0}}{V_{IN}}}={\frac {\rho _{0}Bl}{4\pi S_{D}R_{E}M_{A}S}}H(s)$

其中 $H(s)=sG(s)$。在接下來的部分中，設計方法將集中在 $|H(s)|^{2}$ 而不是 $H(s)$，它由以下公式給出

$|H(s)|^{2}={\frac {\Omega ^{8}}{\Omega ^{8}+\left(a_{3}^{2}-2a_{2}\right)\Omega ^{6}+\left(a_{2}^{2}+2-2a_{1}a_{3}\right)\Omega ^{4}+\left(a_{1}^{2}-2a_{2}\right)\Omega ^{2}+1}}$

$\Omega ={\frac {\omega }{\omega _{0}}}$

這還隱含地忽略了$|H(s)|$前面的常數，因為它們只是縮放了響應，而不會影響頻率響應曲線的形狀。

對齊

確定理想引數的一種流行方法是使用對齊。對齊的概念基於經過充分研究的電子濾波器理論。濾波器開發是一種選擇傳遞函式的極點（以及可能的零點）以滿足特定設計標準的方法。標準是所需的幅度平方傳遞函式的特性，在本例中為$|H(s)|^{2}$。從任何設計標準中，都可以找到$|H(s)|^{2}$的極點（以及可能的零點），然後可以用來計算分子和分母。這是“最佳”傳遞函式，其係數與$|H(s)|^{2}$的引數相匹配，以計算適當的值，這些值將產生滿足標準的設計。

有許多不同型別的濾波器設計，每種設計都有與其相關的權衡。但是，這種設計方法受到$|H(s)|^{2}$結構的限制。特別是，它具有四階高通濾波器的結構，所有零點都在s = 0。因此，只有那些產生僅具有極點的低通濾波器的濾波器設計方法才是可接受的使用方法。從傳統的演算法集中，只有巴特沃斯和切比雪夫低通濾波器僅具有極點。此外，還可以使用另一種稱為準巴特沃斯濾波器的濾波器，它具有與巴特沃斯濾波器相似的特性。這三種演算法都相當簡單，因此它們是最流行的。當這些低通濾波器轉換為高通濾波器時，$s\rightarrow 1/s$變換在分子中產生了$s^{8}$。

有關濾波器理論和這些關係的更多詳細資訊，可以在許多資源中找到，包括[5]。

巴特沃斯對齊

巴特沃斯演算法旨在具有最大平坦的通帶。由於函式的斜率對應於其導數，因此平坦函式的導數將等於零。由於儘可能平坦的通帶是最佳的，因此理想函式在s = 0處將盡可能多地具有等於零的導數。當然，如果所有導數都等於零，那麼該函式將是一個常數，它不執行任何濾波。

通常，更好地檢查所謂的損耗函式。損耗是增益的倒數，因此

$|{\hat {H}}(s)|^{2}={\frac {1}{|H(s)|^{2}}}$

損失函式可用於實現所需特性，然後從損失函式中恢復所需增益函式。

現在，應用所需的巴特沃斯特性，即最大通帶平坦度，損失函式只是一個多項式，其導數在s = 0 時等於零。同時，原始多項式必須是八次方（產生四階函式）。然而，如果[3]，則一階到七階導數可以等於零

$|{\hat {H}}(\Omega )|^{2}=1+\Omega ^{8}\Rightarrow |H(\Omega )|^{2}={\frac {1}{1+\Omega ^{8}}}$

使用高通變換$\Omega \rightarrow 1/\Omega$，

$|H(\Omega )|^{2}={\frac {\Omega ^{8}}{\Omega ^{8}+1}}$

定義$\Omega =\omega /\omega _{3dB}$很方便，因為$\Omega =1\Rightarrow |H(s)|^{2}=0.5$或 -3 dB。此定義允許匹配$|H(s)|^{2}$的係數，當$\omega _{3dB}=\omega _{0}$時描述揚聲器響應。從這種匹配中，得到以下設計方程[1]

$a_{1}=a_{3}={\sqrt {4+2{\sqrt {2}}}}$

$a_{2}=2+{\sqrt {2}}$

準巴特沃斯對齊

與巴特沃斯對齊相比，準巴特沃斯對齊沒有那麼明確的演算法。“準巴特沃斯”這個名稱來源於這些響應的傳遞函式與巴特沃斯傳遞函式非常相似，通常在分母中添加了一些項。這將在下面說明。雖然存在許多型別的準巴特沃斯對齊，但最簡單、最流行的是三階對齊 (QB3)。下面展示了 QB3 幅度平方響應與四階巴特沃斯的比較。

$\left|H_{QB3}(\omega )\right|^{2}={\frac {(\omega /\omega _{3dB})^{8}}{(\omega /\omega _{3dB})^{8}+B^{2}(\omega /\omega _{3dB})^{2}+1}}$

$\left|H_{B4}(\omega )\right|^{2}={\frac {(\omega /\omega _{3dB})^{8}}{(\omega /\omega _{3dB})^{8}+1}}$

請注意，當 $B=0$ 時，即為巴特沃斯對齊。之所以稱這種QB對齊為三階，是因為隨著B的增加，斜率接近3 dec/dec而不是4 dec/dec（如同四階巴特沃斯）。這種現象可以在圖5中看到。

圖5：三階準巴特沃斯響應，$0.1\leq B\leq 3$

將系統響應 $|H(s)|^{2}$ 與 $|H_{QB3}(s)|^{2}$ 相等，可以得到指導設計的方程 [1]

$B^{2}=a_{1}^{2}-2a_{2}$

$a_{2}^{2}+2=2a_{1}a_{3}$

$a_{3}={\sqrt {2a_{2}}}$

$a_{2}>2+{\sqrt {2}}$

切比雪夫對齊

切比雪夫演算法是巴特沃斯演算法的替代方案。對於切比雪夫響應，最大平坦通帶限制被放棄。現在，允許在通帶中出現紋波或波動。這允許更陡峭的過渡或滾降發生。在這種應用中，揚聲器的低頻響應可以擴充套件到巴特沃斯型濾波器所能達到的範圍之外。下面顯示了一個切比雪夫高通響應（紋波為0.5 dB）與相同 $\omega _{3dB}$ 的巴特沃斯高通響應的示例圖。

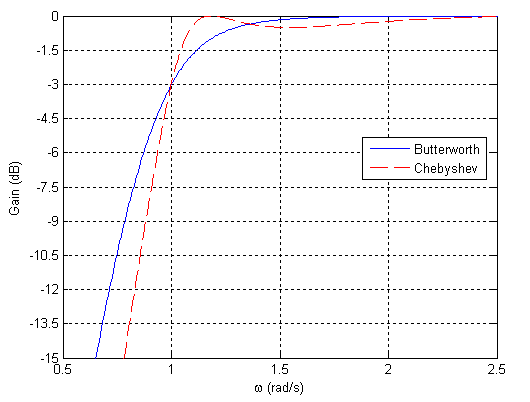
圖6：切比雪夫與巴特沃斯高通響應。

切比雪夫響應由 [4] 定義

$|{\hat {H}}(j\Omega )|^{2}=1+\epsilon ^{2}C_{n}^{2}(\Omega )$

$C_{n}(\Omega )$ 稱為切比雪夫多項式，由 [4] 定義

$C_{n}(\Omega )={\big \lbrace }$	${\rm {{cos}[{\it {{n}{\rm {{cos}^{-1}(\Omega )]}}}}}}$	$|\Omega |<1$
	${\rm {{cosh}[{\it {{n}{\rm {{cosh}^{-1}(\Omega )]}}}}}}$	$|\Omega |>1$

幸運的是，切比雪夫多項式滿足一個簡單的遞迴公式 [4]

$C_{0}(x)=1$

$C_{1}(x)=x$

$C_{n}(x)=2xC_{n-1}-C_{n-2}$

有關切比雪夫多項式的更多資訊，請參見 Wolfram Mathworld: 切比雪夫多項式 頁面。

將高通變換應用於 $|{\hat {H}}(j\Omega )|^{2}$ 的 4 階形式時，所需的響應具有以下形式 [1]

$|H(j\Omega )|^{2}={\frac {1+\epsilon ^{2}}{1+\epsilon ^{2}C_{4}^{2}(1/\Omega )}}$

引數 $\epsilon$ 決定了紋波。特別是，紋波的大小為 $10{\rm {{log}[1+\epsilon ^{2}]}}$ dB，並且可以由設計者選擇，類似於準巴特沃斯情況下的 B。使用 $C_{n}(x)$ 的遞迴公式，

$C_{4}\left({\frac {1}{\Omega }}\right)=8\left({\frac {1}{\Omega }}\right)^{4}-8\left({\frac {1}{\Omega }}\right)^{2}+1$

將此方程應用於 $|H(j\Omega )|^{2}$ [1]，

$\Rightarrow |H(\Omega )|^{2}={\frac {{\frac {1+\epsilon ^{2}}{64\epsilon ^{2}}}\Omega ^{8}}{{\frac {1+\epsilon ^{2}}{64\epsilon ^{2}}}\Omega ^{8}+{\frac {1}{4}}\Omega ^{6}+{\frac {5}{4}}\Omega ^{4}-2\Omega ^{2}+1}}$
$\Omega ={\frac {\omega }{\omega _{n}}}$	$\omega _{n}={\frac {\omega _{3dB}}{2}}{\sqrt {2+{\sqrt {2+2{\sqrt {2+{\frac {1}{\epsilon ^{2}}}}}}}}}$

因此，設計方程變為 [1]

$\omega _{0}=\omega _{n}{\sqrt[{8}]{\frac {64\epsilon ^{2}}{1+\epsilon ^{2}}}}$	$k={\rm {{tanh}\left[{\frac {1}{4}}{\rm {{sinh}^{-1}\left({\frac {1}{\epsilon }}\right)}}\right]}}$	$D={\frac {k^{4}+6k^{2}+1}{8}}$
$a_{1}={\frac {k{\sqrt {4+2{\sqrt {2}}}}}{\sqrt[{4}]{D}}},$	$a_{2}={\frac {1+k^{2}(1+{\sqrt {2}})}{\sqrt {D}}}$	$a_{3}={\frac {a_{1}}{\sqrt {D}}}\left[1-{\frac {1-k^{2}}{2{\sqrt {2}}}}\right]$

選擇正確的對齊方式

在已經展示的所有公式之後，自然而然地會產生一個問題，“我應該選擇哪一個？”請注意，係數$a_{1}$，$a_{2}$，以及$a_{3}$ 並非僅僅與系統響應的引數有關。某些引數的組合確實可能使一種或多種對齊方式失效，因為它們無法實現必要的係數。考慮到這一點，已經制定了通用準則來指導選擇適當的對齊方式。如果要設計一個適合特定不可更改的換能器的箱體，這非常有用。

巴特沃斯對齊的通用準則側重於$Q_{L}$ 和 $Q_{TS}$。由於三個係數$a_{1}$，$a_{2}$，以及$a_{3}$ 是$Q_{L}$，$Q_{TS}$，h，和$\alpha$ 的函式，固定其中一個引數會導致三個方程，這些方程唯一地確定了其他三個引數。在已經給出特定換能器的情況下，$Q_{TS}$ 基本上是固定的。如果已經知道箱體的期望引數，那麼$Q_{L}$ 是一個更好的起點。

如果無法滿足巴特沃斯對齊的嚴格要求，當$Q_{TS}$ 不夠大時，通常應用準巴特沃斯對齊。新增另一個引數B，可以使設計更靈活。

對於$Q_{TS}$ 值太大而無法使用巴特沃斯對齊的情況，通常會選擇切比雪夫對齊。但是，切比雪夫對齊的陡峭過渡也可以用來嘗試在換能器特性可以改變的情況下擴充套件揚聲器的低音響應。

除了這三種流行的對齊方式外，在開發能夠操縱低音反射箱低頻響應的新演算法方面，研究仍在繼續。例如，已經開發出 5 階準巴特沃斯對齊 [6]；它的優點包括改進的低頻擴充套件，以及在低頻下驅動器行程大幅減小，並且通常採用雙聲道或三聲道放大，而它的缺點包括數學有些困難以及電子複雜性（通常需要電子分頻器）。另一個例子 [7] 應用根軌跡技術來實現結果。在當今高效能計算的時代，其他研究人員專注於建立可以修改以實現更平坦響應和更尖銳滾降，或引入準波紋以提供低音訊率提升的計算機最佳化演算法 [8]。

返回工程聲學

參考文獻

[1] Leach, W. Marshall, Jr. Introduction to Electroacoustics and Audio Amplifier Design. 2nd ed. Kendall/Hunt, Dubuque, IA. 2001.

[2] Beranek, L. L. Acoustics. 2nd ed. Acoustical Society of America, Woodbridge, NY. 1993.

[3] DeCarlo, Raymond A. “The Butterworth Approximation.” Notes from ECE 445. Purdue University. 2004.

[4] DeCarlo, Raymond A. “The Chebyshev Approximation.” Notes from ECE 445. Purdue University. 2004.

[5] VanValkenburg, M. E. Analog Filter Design. Holt, Rinehart and Winston, Inc. Chicago, IL. 1982.

[6] Kreutz, Joseph and Panzer, Joerg. "Derivation of the Quasi-Butterworth 5 Alignments." Journal of the Audio Engineering Society. Vol. 42, No. 5, May 1994.

[7] Rutt, Thomas E. "Root-Locus Technique for Vented-Box Loudspeaker Design." Journal of the Audio Engineering Society. Vol. 33, No. 9, September 1985.

[8] Simeonov, Lubomir B. and Shopova-Simeonova, Elena. "Passive-Radiator Loudspeaker System Design Software Including Optimization Algorithm." Journal of the Audio Engineering Society. Vol. 47, No. 4, April 1999.

附錄 A：等效電路引數

名稱	電氣等效	機械等效	聲學等效
音圈電阻	$R_{E}$	$R_{ME}={\frac {(Bl)^{2}}{R_{E}}}$	$R_{AE}={\frac {(Bl)^{2}}{R_{E}S_{D}^{2}}}$
驅動器（揚聲器）質量	參見 $C_{MEC}$	$M_{MD}$	$M_{AD}={\frac {M_{MD}}{S_{D}^{2}}}$
驅動器（揚聲器）懸掛順應性	$L_{CES}=(Bl)^{2}C_{MS}$	$C_{MS}$	$C_{AS}=S_{D}^{2}C_{MS}$
驅動器（揚聲器）懸掛阻力	$R_{ES}={\frac {(Bl)^{2}}{R_{MS}}}$	$R_{MS}$	$R_{AS}={\frac {R_{MS}}{S_{D}^{2}}}$
箱體合規性	$L_{CEB}={\frac {(Bl)^{2}C_{AB}}{S_{D}^{2}}}$	$C_{MB}={\frac {C_{AB}}{S_{D}^{2}}}$	$C_{AB}$
箱體漏氣損失	$R_{EL}={\frac {(Bl)^{2}}{S_{D}^{2}R_{AL}}}$	$R_{ML}=S_{D}^{2}R_{AL}$	$R_{AL}$
埠的聲學質量	$C_{MEP}={\frac {S_{D}^{2}M_{AP}}{(Bl)^{2}}}$	$M_{MP}=S_{D}^{2}M_{AP}$	$M_{AP}$
箱體質量負載	參見 $C_{MEC}$	參見 $M_{MC}$	$M_{AB}$
低頻輻射質量負載	參見 $C_{MEC}$	參見 $M_{MC}$	$M_{A1}$
組合質量負載	$C_{MEC}={\frac {S_{D}^{2}M_{AC}}{(Bl)^{2}}}$ $={\frac {S_{D}^{2}(M_{AB}+M_{A1})+M_{MD}}{(Bl)^{2}}}$	$M_{MC}=S_{D}^{2}(M_{AB}+M_{A1})+M_{MD}$	$M_{AC}=M_{AD}+M_{AB}+M_{A1}$ $={\frac {M_{MD}}{S_{D}^{2}}}+M_{AB}+M_{A1}$

附錄 B：箱體引數公式

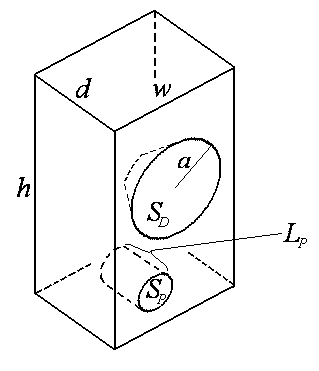
圖 7：低音反射箱體的關鍵尺寸。

基於這些尺寸[1]，

$C_{AB}={\frac {V_{AB}}{\rho _{0}c_{0}^{2}}}$	$M_{AB}={\frac {B\rho _{eff}}{\pi a}}$
$B={\frac {d}{3}}\left({\frac {S_{D}}{S_{B}}}\right)^{2}{\sqrt {\frac {\pi }{S_{D}}}}+{\frac {8}{3\pi }}\left[1-{\frac {S_{D}}{S_{B}}}\right]$	$\rho _{0}\leq \rho _{eff}\leq \rho _{0}\left(1-{\frac {V_{fill}}{V_{B}}}\right)+\rho _{fill}{\frac {V_{fill}}{V_{B}}}$
$V_{AB}=V_{B}\left[1-{\frac {V_{fill}}{V_{B}}}\right]\left[1+{\frac {\gamma -1}{1+\gamma \left({\frac {V_{B}}{V_{fill}}}-1\right){\frac {\rho _{0}c_{air}}{\rho _{fill}c_{fill}}}}}\right]$
$V_{B}=hwd$ (箱體內部總體積)	$S_{B}=wh$ (揚聲器安裝側面的擋板面積)
$c_{air}=$ 空氣在等容過程中的比熱容（約為 $0.718{\frac {\rm {kJ}}{\rm {kg.K}}}$ 在 300 K 時）	$c_{fill}=$ 填充物的等容比熱容（$V_{filling}$）
$\rho _{0}=$ 空氣的平均密度（約為 $1.3{\frac {\rm {kg}}{\rm {m^{3}}}}$ 在 300 K 時）	$\rho _{fill}=$ 填充物的密度
$\gamma =$ 空氣比熱容比（等壓/等容過程）（在 300 K 時約為 1.4）	$c_{0}=$ 空氣中的聲速（約為 344 米/秒）
$\rho _{eff}$ = 箱體的有效密度。如果填充物很少或沒有（在低音反射系統中是可接受的假設，但對於密閉箱體則不可接受），$\rho _{eff}\approx \rho _{0}$