工程聲學/簡諧運動

位置方程

本節介紹如何形成描述彈簧上質量位置的方程。

對於一個由質量 *m* 連線到彈簧一端（彈簧常數為 *s*）的簡單振盪器，恢復力 *f* 可以用以下公式表示：

$f=-sx\,$

其中 *x* 是質量相對於靜止位置的位移。將 *f* 的表示式代入線性動量方程，

$f=ma=m{d^{2}x \over dt^{2}}\,$

其中 *a* 是質量的加速度，我們可以得到

$m{\frac {d^{2}x}{dt^{2}}}=-sx$

或者，

${\frac {d^{2}x}{dt^{2}}}+{\frac {s}{m}}x=0$

注意，振盪頻率 $\omega _{0}$ 由以下公式給出：

$\omega _{0}^{2}={s \over m}\,$

為了解該方程，我們可以假設

$x(t)=Ae^{\lambda t}\,$

則力方程變為

$(\lambda ^{2}+\omega _{0}^{2})Ae^{\lambda t}=0,$

得到方程

$\lambda ^{2}+\omega _{0}^{2}=0,$

解方程求解 $\lambda$

$\lambda =\pm j\omega _{0}\,$

這得出了 *x* 的方程為

$x=C_{1}e^{j\omega _{0}t}+C_{2}e^{-j\omega _{0}t}\,$

注意

$j=(-1)^{1/2}\,$

以及 *C₁* 和 *C₂* 是由系統初始條件決定的常數

如果質量在 *t* = 0 時的位置表示為 *x₀*，那麼

$C_{1}+C_{2}=x_{0}\,$

如果質量在 *t* = 0 時的速度表示為 *u₀*，那麼

$-j(u_{0}/\omega _{0})=C_{1}-C_{2}\,$

解這兩個邊界條件方程得到

$C_{1}={\frac {1}{2}}(x_{0}-j(u_{0}/\omega _{0}))$

$C_{2}={\frac {1}{2}}(x_{0}+j(u_{0}/\omega _{0}))$

然後位置由下式給出

$x(t)=x_{0}cos(\omega _{0}t)+(u_{0}/\omega _{0})sin(\omega _{0}t)\,$

此方程也可以透過假設 *x* 具有以下形式找到

$x(t)=A_{1}cos(\omega _{0}t)+A_{2}sin(\omega _{0}t)\,$

並應用相同的初始條件，

$A_{1}=x_{0}\,$

$A_{2}={\frac {u_{0}}{\omega _{0}}}\,$

這導致了相同的位移方程

$x(t)=x_{0}cos(\omega _{0}t)+(u_{0}/\omega _{0})sin(\omega _{0}t)\,$

返回主頁

位移方程的替代形式

如果A₁和A₂是以下形式

$A_{1}=Acos(\phi )\,$ $A_{2}=Asin(\phi )\,$

那麼位移方程可以寫成

$x(t)=Acos(\omega _{0}t-\phi )\,$

透過應用初始條件 (x(0)=x₀, u(0)=u₀) 可以發現

$x_{0}=Acos(\phi )\,$

${\frac {u_{0}}{\omega _{0}}}=Asin(\phi )\,$

如果將這兩個方程平方後相加，則可以發現

$A={\sqrt {x_{0}^{2}+({\frac {u_{0}}{\omega _{0}}})^{2}}}\,$

如果找到這兩個相同方程的差，則結果是

$\phi =tan^{-1}({\frac {u_{0}}{x_{0}\omega _{0}}})\,$

位移方程也可以寫成虛位移方程的實部

$\mathbf {Re} [x(t)]=x(t)=Acos(\omega _{0}t-\phi )\,$

根據尤拉公式 (e^jφ = cosφ + jsinφ)，x(t) 具有以下形式

$x(t)=Ae^{j(\omega _{0}t-\phi )}\,$

示例 1.1

已知: 兩個彈簧的剛度為 $s$，兩個物體的質量為 $M$

求解: 以下系統草圖的固有頻率

1. 

   簡諧振盪器-1.2.1.a

$s_{TOTAL}=s+s{\text{ (springs are in parallel)}}$

$\omega _{0}={\sqrt {\frac {s_{TOTAL}}{m_{TOTAL}}}}={\sqrt {\frac {2s}{M}}}$

$\mathbf {f_{0}} ={\frac {\omega _{0}}{2\pi }}=\mathbf {{\frac {1}{2\pi }}{\sqrt {\frac {2s}{M}}}}$

2. 

   簡諧振盪器-1.2.1.b

$\omega _{0}={\sqrt {\frac {s_{TOTAL}}{m_{TOTAL}}}}={\sqrt {\frac {s}{2M}}}$

$\mathbf {f_{0}} ={\frac {\omega _{0}}{2\pi }}=\mathbf {{\frac {1}{2\pi }}{\sqrt {\frac {s}{2M}}}}$

3. 

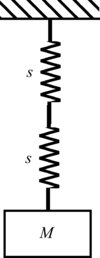   簡單振盪器-1.2.1.c

$\mathbf {1.} {\text{ }}s(x_{1}-x_{2})=sx_{2}$

$\mathbf {2.} {\text{ }}-s(x_{1}-x_{2})=m{\frac {d^{2}x}{dt^{2}}}$

${\frac {d^{2}x_{1}}{dt^{2}}}+{\frac {s}{2m}}x_{1}=0$

$\omega _{0}={\sqrt {\frac {s}{2m}}}$

$\mathbf {f_{0}={\frac {1}{2\pi }}{\sqrt {\frac {s}{2m}}}}$

4. 

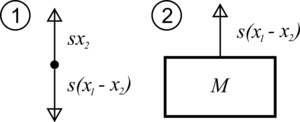
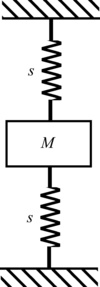   簡單振盪器-1.2.1.d

$\omega _{0}={\sqrt {\frac {2s}{m}}}$

$\mathbf {f_{0}={\frac {1}{2\pi }}{\sqrt {\frac {2s}{m}}}}$

返回主頁