工程聲學/換能器 - 揚聲器

聲學換能器

聲學換能器的目的是將電能轉換為聲能。聲學換能器有很多變體，例如靜電式、動鐵式和動圈式揚聲器。本文重點介紹動圈式揚聲器，因為它們是最常用的聲學換能器型別。首先，簡要討論了典型的動圈式換能器的物理結構和原理。其次，以教程的方式介紹了組成揚聲器的每個元素的機電聲建模，以加強和補充之前在其他部分中看到的關於機電模擬和機聲模擬的理論。第三，分析了等效電路，引入了Thiele-Small 引數背後的理論，這些引數在設計揚聲器箱體時非常有用。還包括了一種實驗確定 Thiele-Small 引數的方法。

動圈式揚聲器結構和原理

經典的動圈式揚聲器驅動器可以分為三個關鍵部分

1）磁電機系統，包括永磁體、中心極和音圈，它們共同作用，透過電流在振膜上產生機械力。

2）揚聲器錐盆系統，包括振膜和防塵罩，使機械力轉換為聲壓；

3）揚聲器懸掛系統，包括蜘蛛和環繞，防止振膜因過度偏移而破裂，只允許平移運動，並傾向於使振膜回到其靜止位置。

以下插圖顯示了一個典型的動圈式永磁揚聲器的剖檢視。一個線圈機械地耦合到一個振膜（也稱為錐盆），並位於由磁鐵產生的固定磁場中。當電流流過線圈時，會發出相應的磁場，與磁鐵的固定場相互作用，從而對線圈施加力，將其推離或朝向磁鐵。由於錐盆與線圈機械耦合，它將推或拉動它所面對的空氣，導致壓力變化併發出聲波。

圖 1：典型的動圈式揚聲器的橫截面圖

可以獲得一個等效電路來對揚聲器進行建模，使其成為一個集總系統。該電路可用於驅動完整揚聲器系統的設計，包括箱體，有時甚至與驅動器特性匹配的放大器。下一部分展示瞭如何獲得這種等效電路。

機電聲等效電路

只要每個元素作為一個整體運動，像揚聲器這樣的機電聲系統就可以建模為等效電氣電路。這在低頻或系統尺寸遠小於感興趣波長的情況下通常是正確的。為了獲得揚聲器的完整模型，必須對組成揚聲器驅動器的電氣、機械和聲學子系統之間的相互作用和特性進行建模。以下部分詳細介紹瞭如何從放大器開始，到空氣呈現的聲學負載結束，獲得該電路。類似的推導可以在[1]或[2]中找到。

電氣子系統

系統中的電氣部分由驅動放大器和音圈組成。大多數放大器可以近似為串聯在放大器輸出阻抗中的理想電壓源。音圈表現出電感和電阻，可以作為電路直接建模。

圖 2：放大器和揚聲器電氣元件作為電路建模

電氣到機械子系統

當揚聲器接收到電訊號時，音圈和磁鐵將電流轉換為力。類似地，電壓與速度相關。這種電氣側與機械側之間的關係可以用一個變壓器來建模。

${\tilde {f_{c}}}=Bl{\tilde {i}}$; ${\tilde {u_{c}}}={\dfrac {\tilde {e}}{Bl}}$

圖 3：將轉換從電阻抗建模為機械遷移率類比的變壓器

機械子系統

在最初的近似中，動圈式揚聲器可以被認為是一個質量-彈簧系統，其中振膜和音圈構成質量，蜘蛛和懸邊構成彈簧元件。懸掛中的損耗可以建模為一個電阻。

圖 4：阻抗和遷移率型別的質量彈簧系統和相關電路類比。

運動方程給出我們 

${\tilde {f_{c}}}=R_{m}{\tilde {u_{c}}}+{\dfrac {\tilde {u_{c}}}{j\omega C_{MS}}}+j\omega M_{MD}{\tilde {u_{c}}}$ ${\dfrac {\tilde {f_{c}}}{\tilde {u_{c}}}}=R_{m}+{\dfrac {1}{j\omega C_{MS}}}+j\omega M_{MD}$

這產生了以串聯 RLC 電路形式的機械阻抗型別類比。還可以透過數學操作獲得並聯 RLC 電路以獲得遷移率類比

${\dfrac {\tilde {u_{c}}}{\tilde {f_{c}}}}={\dfrac {1}{R_{m}+{\dfrac {1}{j\omega C_{MS}}}+j\omega M_{MD}}}$ ${\dfrac {\tilde {u_{c}}}{\tilde {f_{c}}}}={\dfrac {1}{{\dfrac {1}{G_{m}}}+{\dfrac {1}{j\omega C_{MS}}}+{\dfrac {1}{\dfrac {1}{j\omega M_{MD}}}}}}$

這表示以並聯 RLC 電路形式的機械遷移率型別類比，其中分母元素分別是並聯電導、電感和順從性。

機械到聲學子系統

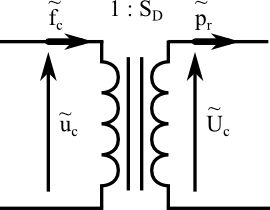
揚聲器的振膜可以被認為是一個活塞，它對它所面對的空氣進行推拉，將機械力和速度轉換為聲壓和體積速度。方程如下：

${\tilde {P_{d}}}={\dfrac {\tilde {f_{c}}}{\tilde {S_{D}}}}$; ${\tilde {U_{c}}}={\tilde {u_{c}}}{S_{D}}$

這些方程可以用一個變壓器來模擬。

圖 5: 模擬揚聲器振膜執行的從機械移動性到聲學移動性類比的變換的變壓器。

聲學子系統

揚聲器振膜上的空氣負載呈現的阻抗既有由於聲音輻射引起的電阻性阻抗，也有由於正在徑向推動但沒有對遠場聲音輻射做出貢獻的空氣質量引起的電抗性阻抗。振膜上的空氣負載可以用阻抗或導納來模擬。在 [1]、[2] 或 [3] 中可以找到特定值和近似值。請注意，空氣負載取決於揚聲器的安裝條件。如果揚聲器安裝在擋板上，則振膜兩側的空氣負載將相同。然後，如果一側的空氣負載是 $Y_{AR}$ 在導納類比中，那麼總空氣負載就是 $Y_{AR}/2$，因為兩個負載都是並聯的。

完整的電-機-聲等效電路

使用電阻抗、機械移動性和聲學導納，可以得到以下等效電路，該電路模擬整個揚聲器驅動單元。

圖 6: 揚聲器驅動單元的完整電-機-聲等效電路。

可以透過用與負載變壓器具有相同阻抗的等效負載替換變壓器和連線的負載來簡化該電路。圖 7 顯示了這一點的一個例子，其中聲學和電氣負載和電源已“轉移”到機械側。

圖 7: 揚聲器驅動單元的機械等效電路建模。

這樣做的好處是，我們可以直接將電氣測量值與電路中的元素相關聯。這將使我們能夠隨後獲得模型不同元件的值，並將該模型與實際揚聲器驅動器匹配。我們可以透過使用諾頓定理並將串聯電氣元件和電壓源轉換為等效電流源和並聯電氣元件來進一步簡化該電路。然後，使用稱為“點法”的技術（在 解決方案方法：電-機械類比 部分介紹），我們可以得到一個單環串聯電路，它是先前使用諾頓定理獲得的並聯電路的對偶。如果我們主要對揚聲器的低頻行為感興趣，就像使用集中元件建模時應該的那樣，我們可以忽略音圈電感的效應，該電感僅在高頻下才有效應。此外，低頻下的空氣負載阻抗類似於質量，可以用一個簡單的電感 $M_{M1}$ 來模擬。這將導致一個簡化的低頻模型等效電路（如圖 8 所示），它比圖 7 中的電路更容易操作。請注意，此電路使用的類比是阻抗型別的。

圖 8: 揚聲器驅動單元的低頻近似機械等效電路。

其中 $M_{M1}=2.67a^{3}\rho$ 如果 $a$ 是揚聲器的半徑，而 $\rho$ 是空氣的密度。在這種情況下，振膜和音圈的質量 $M_{MS}$ 和對振膜進行空氣質量負載的 $2M_{M1}$ 可以合併到一個元素中。

$M_{MS}=M_{MD}+2M_{M1}$

Thiele-Small 引數

理論

揚聲器驅動單元的完整低頻行為可以用六個引數建模，稱為 Thiele-Small 引數。這些引數中的大多數是來自圖 8 電路的方程的代數運算結果。揚聲器驅動器製造商很少直接提供機電聲引數，而是會在資料表中提供 Thiele-Small 引數，但從一種引數轉換到另一種引數非常簡單。Thiele-Small 引數如下所示

1. $R_{e}$，音圈直流電阻；

2. $Q_{ES}$，電氣品質因數；

3. $Q_{MS}$，機械品質因數；

4. $f_{s}$，揚聲器諧振頻率；

5. $S_{D}$，振膜的有效表面積；

6. $V_{AS}$，等效懸掛體積：與揚聲器驅動器的懸掛具有相同聲學順應性的空氣體積。

這些引數可以直接從圖 8 的低頻近似電路中關聯，其中 $R_{e}$ 和 $S_{D}$ 是明確的。

$Q_{MS}={\dfrac {1}{R_{MS}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$； $Q_{ES}={\dfrac {R_{g}+R_{e}}{(Bl)^{2}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$ ; $f_{s}={\dfrac {1}{2\pi {\sqrt {M_{MS}C_{MS}}}}}$； $V_{AS}=C_{MS}S_{D}^{2}\rho c^{2}$

其中 $\rho c^{2}$ 是空氣的體積模量。因此，如果給定了 Thiele-Small 引數，則可以使用以下公式提取圖 8 電路中每個元件的值

$C_{MS}={\dfrac {V_{AS}}{S_{D}^{2}\rho c^{2}}}$; $M_{MS}={\dfrac {1}{(2\pi f_{s})^{2}C_{MS}}}$; $R_{MS}={\dfrac {1}{Q_{MS}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$; $Bl={\sqrt {\dfrac {R_{e}}{2\pi f_{s}Q_{ES}C_{MS}}}}$; $M_{MD}=M_{MS}-2M_{M1}$;

測量

許多方法可以用來測量驅動器的Thiele-Small引數。如果製造商沒有提供Thiele-Small引數，有時需要測量。此外，給定揚聲器的實際Thiele-Small引數可能與標稱值存在顯著差異。本節中描述的方法來自[2]。請注意，對於此方法，揚聲器被認為是安裝在無限大的擋板上。在實踐中，直徑為揚聲器直徑四倍的擋板就足夠了。也可以在沒有擋板的情況下進行測量：空氣質量負載只會減少一半，並且可以輕鬆地進行調整。此方法的設定包括一個FFT分析儀或用於獲取阻抗曲線的工具。也可以使用可變頻率的訊號發生器和交流表。

圖9：測量揚聲器驅動單元阻抗的簡單實驗裝置 $Z_{spk}=R{\dfrac {V_{spk}}{V_{s}\left(1-{\dfrac {V_{spk}}{V_{s}}}\right)}}$ 圖10：典型的揚聲器驅動單元阻抗曲線

一旦測量了揚聲器的阻抗曲線，$R_{e}$ 和 $f_{s}$ 可以透過觀察阻抗值的低頻漸近線和共振峰的中心頻率來直接識別。如果識別出 $Z_{spk}={\sqrt {R_{e}R_{c}}}$ 的頻率為 $f_{l}$ 和 $f_{h}$，可以計算出Q因子。

$Q_{MS}={\dfrac {f_{s}}{f_{h}-f_{l}}}{\sqrt {\dfrac {R_{c}}{R_{e}}}}$ $Q_{ES}={\dfrac {Q_{MS}}{{\dfrac {R_{c}}{R_{e}}}-1}}$

$S_{D}$ 可以簡單地用 $\pi a^{2}$ 近似，其中 $a$ 是揚聲器驅動器的半徑。最後一個剩餘的 Thiele-Small 引數，$V_{AS}$ 測量起來稍微棘手一點。想法是增加揚聲器驅動單元的質量或降低其順性，並記錄共振頻率的變化。如果已知的質量 $M_{x}$ 新增到揚聲器振膜上，新的共振頻率將是

$f_{s}^{'}={\dfrac {1}{2\pi {\sqrt {(M_{MS}+M_{x})C_{MS}}}}}$

等效懸掛體積可以透過以下方法獲得

$V_{AS}=\left(1-{\dfrac {f_{s}^{'2}}{f_{s}^{2}}}\right){\dfrac {S_{D}^{2}\rho c^{2}}{(2\pi f_{s}^{'})^{2}M_{x}}}$

因此，所有用於模擬揚聲器驅動單元低頻特性的 Thiele-Small 引數都可以從一個相當簡單的設定中獲得。這些引數在揚聲器箱體設計中起著至關重要的作用。

數值示例

本節介紹了從阻抗曲線獲取 Thiele-Small 引數的數值示例。本節中提供的阻抗曲線是使用真實低音揚聲器的標稱 Thiele-Small 引數透過模擬獲得的。首先，這些 Thiele-Small 引數使用之前介紹的方程轉換為電-機-聲電路。其次，該電路被視為黑盒子，並使用了提取 Thiele-Small 引數的方法。該模擬的目的是使用實際值逐步展示該方法，以便讀者能夠更加熟悉該過程、值的大小以及執行此類測量時應期望的結果。

在本模擬中，半徑為 $a=6.55cm$ 的揚聲器安裝在足夠大的擋板上，以充當無限擋板。其阻抗被獲得並繪製在圖 11 中，其中重要的游標已經放置。

圖 11：低音揚聲器阻抗曲線的模擬測量

低頻漸近線立即被識別為 $Re=6.6\Omega$。共振清晰，位於 $fs=33Hz$。該頻率下的阻抗值約為 $66\Omega$。這產生了 ${\sqrt {R_{e}R_{c}}}=20.8\Omega$，它出現在 $f_{l}=19.5Hz$ 和 $f_{h}=52.5Hz$。有了這些資訊，我們可以計算一些 Thiele-Small 引數。

$Q_{MS}={\dfrac {f_{s}}{f_{h}-f_{l}}}{\sqrt {\dfrac {R_{c}}{R_{e}}}}={\dfrac {33}{52.5-19.5}}*{\sqrt {\dfrac {66}{6.6}}}=3.1$ $Q_{ES}={\dfrac {Q_{MS}}{{\dfrac {R_{c}}{R_{e}}}-1}}={\dfrac {3.1}{{\dfrac {66}{6.6}}-1}}=0.35$

下一步，將質量為 $M_{x}=10g$ 的物體固定在揚聲器振膜上。這將改變共振頻率，併產生新的阻抗曲線，如圖 12 所示。

圖 12：低音揚聲器阻抗曲線的模擬測量 $S_{D}=\pi a^{2}=0.0135m^{2}$ $V_{AS}=\left(1-{\dfrac {27.5^{2}}{33^{2}}}\right){\dfrac {0.0135^{2}*1.18*344^{2}}{(2\pi 27.5)^{2}*0.01}}=0.0272m^{3}$

一旦獲得所有六個 Thiele-Small 引數，就可以計算圖 6 或 7 中電機械聲學電路模型元素的值。然後，就可以開始設計音箱。這將在應用部分 密封箱低音炮設計 和 低音反射箱設計 中討論。

參考文獻

[1] Kleiner，Mendel。電聲學。CRC 出版社，2013 年。

[2] Beranek，Leo L. 和 Tim Mellow。聲學：聲場和換能器。學術出版社，2012 年。

[3] Kinsler，Lawrence E. 等。聲學基礎，第 4 版。Wiley-VCH，1999 年。

[4] Small，Richard H. “直接輻射揚聲器系統分析”。《音訊工程學會期刊》20.5 (1972)：383-395。