工程聲學/吸聲結構和材料

介紹

噪聲可以定義為不需要的聲音。在許多情況下和應用中，降低噪聲水平非常重要。聽力損失只是持續暴露於過高噪聲水平的其中一個影響。噪聲會干擾睡眠和說話，並造成不適和其他非聽覺影響。此外，高水平的噪聲和振動會導致許多工業裝置的結構故障以及使用壽命縮短。例如，在控制閥中，由流動不穩定引起的振動有時會損壞控制系統的反饋，從而導致極端的振盪。透過觀察政府為了限制社會噪聲排放而制定的法規，可以很好地理解噪聲問題的重要性。工業機械、空/陸地交通運輸和建築活動被認為是噪聲產生或所謂的“噪聲汙染”的主要貢獻者。

噪聲控制機制

• 主動噪聲控制

透過電聲方法修改和消除聲場稱為主動噪聲控制。主動控制有兩種方法。第一種是利用執行器作為聲源產生完全異相訊號以消除干擾。第二種方法是使用柔性和振動彈性材料來輻射干擾干擾的聲場並最小化整體強度。後一種方法稱為主動結構聲學控制 (ASAC)。

• 被動噪聲控制

被動噪聲控制是指那些透過修改靠近聲源的環境來抑制聲音的方法。由於此類方法不需要輸入功率，因此被動噪聲控制通常比主動控制更便宜，但效能僅限於中高頻。主動控制在低頻工作良好，因此可以將兩種方法結合起來用於寬頻噪聲抑制。

圖 1：噪聲控制機制

吸聲

聲波撞擊任意表面時，會發生反射、透射或吸收；進入反射、透射或吸收的能量多少取決於表面的聲學特性。反射聲可以被大的平坦表面幾乎完全地重新定向，也可以被漫反射表面散射。當大量反射聲在空間和時間上發生散射時，這種狀態稱為漫反射，涉及的表面通常稱為漫射器。吸收的聲能可以被透射或消散。圖 2 顯示了表面-波相互作用的簡單示意圖。

圖 2：表面-聲相互作用 - 吸收（左）、反射（中）和漫射（右）

聲能透過粘性和熱機制的共同作用而消散。吸聲器用於消散聲能，以最大程度地減少其反射。 吸聲係數 $\alpha$ 是一個常用的測量材料吸聲效能的量，已知它是入射波頻率的函式。它被定義為材料吸收的能量與入射到其表面的能量之比。

吸聲係數

吸聲係數可以數學表達如下

$\alpha =1-{\frac {I_{R}}{I_{I}}}$

其中 α，$I_{R}$ 和 $I_{I}$ 分別代表吸聲係數、反射聲的單邊強度和入射聲的單邊強度。

從上面的公式可以看出，材料的吸聲係數在 0 到 1 之間變化。有幾種標準方法可以測量吸聲係數。在一種常用的方法中，使用配備了兩個麥克風的平面波阻抗管。實驗裝置和尺寸符合 ASTM E1050/ISO 10534-2。 （圖 3）該方法透過評估傳遞函式， ${\hat {h}}(f)$ 在兩個相隔 s 的麥克風之間，以及從樣品到麥克風的距離 l 來獲得吸聲係數，使用以下公式

${\hat {h}}={\frac {\hat {p_{1}}}{\hat {p_{2}}}}$

${\hat {r}}={\frac {{\hat {h}}-e^{-jks}}{e^{jks}+{\hat {h}}}}$

$\alpha =1-|{\hat {r}}|^{2}$

其中，${\hat {p_{1}}},{\hat {p_{2}}}$ 分別是麥克風 1 和麥克風 2 測量的復壓振幅。k 是波數，s 是麥克風的間距，$\alpha$ 是吸聲係數。

根據標準技術， 頻率受麥克風間距和管徑的限制。還建議 $0.05{\frac {c}{s}}<f<0.45{\frac {c}{s}}$ 以確保平面波傳播。商業吸聲材料的係數以噪聲衰減係數 (NRC) 表示，指的是 250 Hz、500 Hz、1000 Hz 和 2000 Hz 吸聲係數的平均值。表 1 列出了建築物中使用的一些聲學隔音材料的平均值。根據其結構和材料結構，吸聲器分為 非多孔 和 多孔 吸聲器。

圖 3：雙麥克風法獲得吸聲係數

表 1 - 常用吸聲材料的吸聲係數

材料	吸聲係數
6 毫米軟木板	0.1-0.2
6 毫米多孔橡膠板	0.1-0.2
12 毫米纖維板	0.3-0.4
50 毫米礦渣棉或玻璃絲	0.8-0.9
硬木	0.3
100 毫米礦棉	0.65

非多孔吸聲器（吸聲共振器）

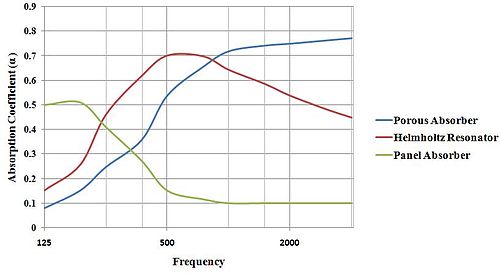
在工業應用中，有兩種常見的非多孔吸聲器。面板（膜）共振器 和 亥姆霍茲共振器。面板吸聲器是輕質、薄而沒有孔洞的板材或膜，這些板材或膜經過調諧，可以在特定頻率範圍內吸收聲波。面板對快速成形的結構阻力導致吸聲。面板吸聲器由其幾何形狀和結構振動特性決定。亥姆霍茲共振器或腔體吸聲器是具有非常小孔的穿孔結構；一個例子是用於飛機發動機機架內部的吸聲襯層，用於抑制壓縮和燃燒階段產生的噪聲排放。類似的結構應用於通風和空調系統中使用的風機和通風機。開口尺寸、頸部長度和腔體體積決定了共振器的共振頻率，因此也決定了吸聲效能。

多孔吸聲器

多孔吸聲器對應於聲波在相互連線的孔隙網路中傳播的材料，因此粘性熱相互作用導致聲能耗散並轉化為熱能。礦渣棉、玻璃纖維或高孔隙率泡沫等吸聲處理可減少反射聲。多孔吸聲器實際上是熱工材料，通常不是有效的隔音屏障。與工作聲波長相比，需要相當大的厚度，這使得多孔吸聲器在低頻時效率低下且不切實際。

圖 2：不同吸聲體吸聲係數的典型變化

多孔吸聲體的物理特性

聲音在多孔材料中的傳播是一個受多孔介質物理特性控制的現象，即孔隙率 ($\phi$)、曲折度 (q)、流動阻抗 ($\sigma$)、粘性特徵長度 ($\Lambda$) 和熱特徵長度 ($\Lambda '$).

• 孔隙率

定義為相互連通的空隙體積（開放孔隙中的空氣體積）與總體積的比率。大多數商業吸聲體具有高孔隙率（大於 0.95）。孔隙率越高，固體-流體相之間的相互作用就越容易，從而導致更多的聲能衰減。

$\phi ={\frac {V_{0}}{V_{T}}}$

$V_{0}$ = 空隙空間的體積。

$V_{T}$ = 多孔材料的總體積。

• 曲折度

該物理特性對應於多孔材料內部孔隙網路的“非直線性”。它顯示了多孔材料如何有效地阻止穿過多孔介質的直接流動。路徑越複雜，波與吸聲體接觸的時間就越長，因此能量耗散越多，吸聲能力就越強。如果多孔吸聲體不導電，一種測量方法是將吸聲體浸泡在導電流體中並測量飽和樣品的電阻率，$R_{s}$，並與流體本身的電阻率進行比較，$R_{f}$，則曲折度可以表示如下

$q=\phi {\frac {R_{s}}{R_{f}}}$

• 流動阻抗

驅動單位流量透過材料所需的壓降可以與多孔吸聲體內傳播聲波的粘性損失相關聯，並表示為流動阻抗。對於各種多孔材料，流動阻抗是聲吸收的主要因素。流動阻抗的單位是 $N.s/m^{4}$ 或 $Rayls/m$，定義為靜態壓降 $\Delta P$ 與體積流量 (U) 的比值，對於小的樣品厚度 (d)。

$\sigma ={\frac {\Delta P}{Ud}}$

• 特徵長度

另外兩個重要的微觀結構特性是特徵粘性長度$\Lambda$和特徵熱長度$\Lambda$’，它們分別導致粘性耗散和熱耗散。前者與較小的孔隙相關，後者與多孔聚集體的較大孔隙相關。熱長度$\Lambda '$是連通孔隙中體積與表面積之比的兩倍。它是一個幾何量，可以直接測量。粘性長度，$\Lambda$，幾乎相同，但每個積分都乘以孔隙內流體速度v的平方，因此無法直接測量。

$\Lambda '=2{\frac {\int dV}{\int dS}}$

$\Lambda =2{\frac {\int v_{fluid}^{2}dV}{\int v_{fluid}^{2}dS}}$

多孔吸聲材料的聲學建模

剛性多孔吸聲材料中的波動方程

從質量守恆和動量守恆的線性化方程推導的平面波方程應該修改，以考慮孔隙率、曲折度和流動阻力的影響。修改後的波動方程控制著可壓縮氣體填充的剛性多孔材料中的聲傳播，其表示式為

${\frac {\partial ^{2}P}{\partial x^{2}}}-({\frac {q\rho _{0}}{k_{eff}}})*{\frac {\partial ^{2}P}{\partial t^{2}}}-({\frac {\sigma \phi }{k_{eff}}})*{\frac {\partial p}{\partial t}}=0$

其中，p = 材料孔隙內的聲壓

$\rho _{0}$ = 可壓縮氣體的密度

$k_{eff}$ = 氣體的有效體積模量

q = 曲折度

$\phi$ = 孔隙率

$\sigma$ = 流動阻力

吸聲多孔層的聲學特性也可以從其基本聲學量進行研究：復波數和特徵阻抗。這些量是作為修改後的平面波方程解的一部分獲得的，可用於確定吸聲係數和表面阻抗。復波數和表面阻抗最實用和最常見的值基於半經驗方法，並使用迴歸分析進行關聯。Delany 和 Bazely 建議了一種重要的關聯

$k'=\alpha +j\beta ={\frac {\omega }{c}}[1+0.0978({\frac {\rho _{0}f}{\sigma }})^{-0.700}-j0.189({\frac {\rho _{0}f}{\sigma }})^{-0.595}]$

$z'=R+jX=\rho _{0}c[1+0.0571({\frac {\rho _{0}f}{\sigma }})^{-0.754}-j0.087({\frac {\rho _{0}f}{\sigma }})^{-0.732}]$

其中，f = 頻率 σ = 流阻

有效密度

假設吸聲材料的孔隙網路為剛性框架，固體相完全靜止，框架體積模量遠大於可壓縮氣體的體積模量，因此可以使用具有複雜有效流體密度和複雜有效體積模量的流體波動方程對其進行建模。在這種情況下，動態密度考慮了粘性損耗，而動態體積模量考慮了熱損耗。Johnson 等人提出了有效密度與動態曲折度的關係。

$\rho _{eff}=q(1+{\frac {\sigma \phi }{j\omega \rho _{0}q}}G(\omega ))\rho _{0}$

$G(\omega )={\sqrt {1+j{\frac {4q^{2}\mu \rho _{0}\omega }{\sigma ^{2}\Lambda ^{2}\phi ^{2}}}}}$

其中，

μ = 氣體粘度

ω = 2πf

有效體積模量

另一個影響吸聲材料中聲傳播的因素是材料中的熱相互作用，這是由於可壓縮流體中傳播的聲波前沿與固體相之間的熱交換造成的。Champoux 和 Allard .，引入了函式 $G'(\omega )$ 來評估氣體的有效體積模量。正如在下面的公式中觀察到的那樣，這將是熱特徵長度 ($\Lambda '$).

$k_{eff}={\frac {\gamma p_{0}}{\gamma -(\gamma -1)(1-j{\frac {8\mu }{\Lambda '^{2}Pr^{2}\omega \rho _{0}}}G'(\omega ))\rho _{0}}}$

$G'(\omega )={\sqrt {1+j{\frac {\Lambda '^{2}Pr^{2}\omega \rho _{0}}{16\mu }}}}$

其中，

γ = 氣體比熱比（對於空氣約為 1.4）

Pr = 流體普朗特數